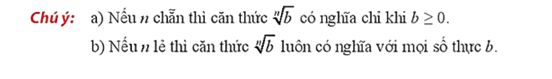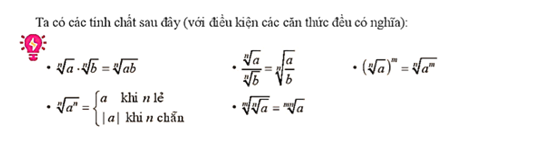1. Bài giảng: Phép tính lũy thừa với số mũ thực
Phép tính lũy thừa với số mũ thực
1. Lũy thừa với số mũ nguyên

- 00 và 0−n không có nghĩa.
- Nếu a>1 thì am>an khi và chỉ khi m>n.
- Nếu 0<a<1 thì am>an khi và chỉ khi m<n.
2. Căn bậc n
- Định nghĩa: Cho số thực a và số nguyên dương n≥2 . Số b được gọi là căn bậc n của số a nếu bn=a.
- Với n chẵn, ta xét ba trường hợp sau:
- Với n lẻ, a∈R : Có duy nhất một căn bậc n của a , ký hiệu là n√a.
3. Lũy thừa với số mũ hữu tỉ
- Cho số thực a>0 và số hữu tỉ r=nm , trong đó m,n∈Z,n>0.
- Lũy thừa của a với số mũ r , kí hiệu là ar , được xác định bởi ar=anm=n√am
4. Lũy thừa với số mũ thực
- Giới hạn của dãy số (arn) gọi là lũy thừa của số thực dương a với số mũ α . Kí hiệu là: aα=limarn với α=n→+∞limrn
5. Tính chất của phép tính lũy thừa
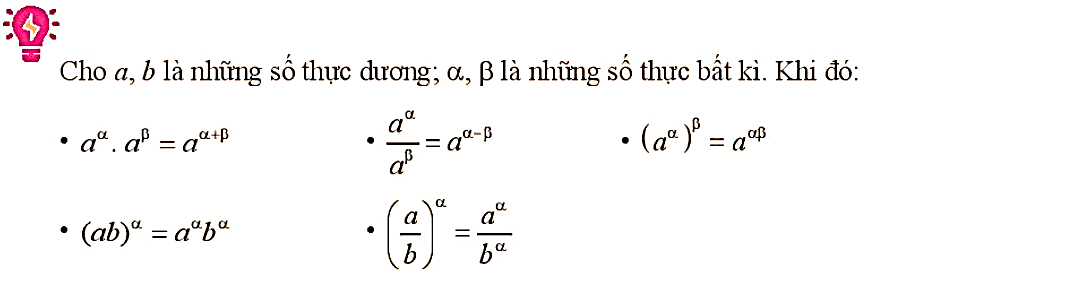
2. Ví dụ minh hoạ: Phép tính lũy thừa với số mũ thực
Ví dụ 1:
Cho a>1 .
Mệnh đề nào sau đây là đúng ?
Lời giải:
a√51=a−√5<a−√3(−√5<−√3)
Ví dụ 2:
So sánh hai số m và n nếu (91)m>(91)n
Lời giải:
Ta có:
91<1;(91)m>(91)n⇒m<n
3. Luyện tập củng cố: Phép tính lũy thừa với số mũ thực
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay