Phương trình lượng giác 

1. Phương trình tương đương

• Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

Chú ý: Để giải phương trình, ta thường biến đổi phương trình đó thành một phương trình tương đương đơn giản hơn. Các phép biến đổi như vậy được gọi là các phép biến đổi tương đương. Ta có một số phép biến đồi tương đương thường sử dụng sau:

• Cộng hoặc trừ hai vế của phương trình với cùng một số hoặc cùng một biểu thức mà không làm thay đổi điều kiện của phương trình.
• Nhân hoặc chia hai vế của phương trình với cùng một số khác 0 hoặc cùng một biểu thức luôn có giá trị khác 0 mà không làm thay đổi điều kiện của phương trình.
• Để chi sự tương đương của các phương trình, người ta dùng kí hiệu " ⇔  ".

2. Phương trình sinx = m

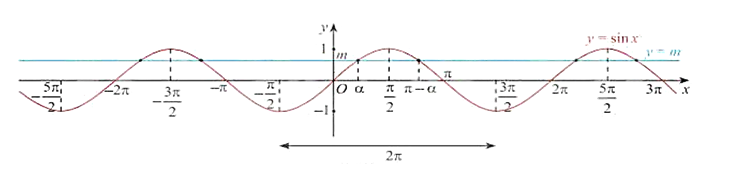
• Xét phương trình sinx=m. 
• Nếu ∣m∣>1 thì phương trình vô nghiệm.
• Nếu ∣m∣≤1 thì phương trình có nghiệm:

 x=α+k2π,k∈Z

và x=π−α+k2π,k∈Z 

với α là góc thuộc [−2π​;2π​] sao cho sinα=m. 

Chú ý: Một số trường hợp đặc biệt:

• sinx=1⇔x=2π​+k2π,k∈Z; 
• sinx=−1⇔x=−2π​+k2π,k∈Z; 
• sinx=0⇔x=kπ,k∈Z. 

• sinu=sinv⇔u=v+k2π,k∈Z  hoặc u=π−v+k2π,k∈Z. 
• sinx=sina∘⇔x=a∘+k360∘,k∈Z  hoặc x=180∘−a∘+k360∘,k∈Z. 

3. .Phương trinh cosx = m

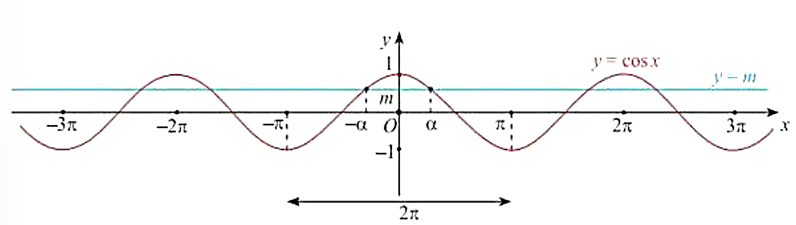
• Xét phương trình cosx=m. 
• Nếu ∣m∣>1  thì phương trình vô nghiệm.
• Nếu ∣m∣≤1  thì phương trình có nghiệm:

x=α+k2π,k∈Z 

Và x=−α+k2π,k∈Z, 

với α  là góc thuộc [0;π]  sao cho cosα=m. 

Chú ý: Một số trường hợp đặc biệt:

• cosx=1⇔x=k2π,k∈Z; 
• cosx=−1⇔x=π+k2π,k∈Z; 
• cosx=0⇔x=2π​+kπ,k∈Z. 

• cosu=cosv⇔u=v+k2π,k∈Z  hoặc u=−v+k2π,k∈Z. 
• cosx=cosa∘⇔x=a∘+k360∘,k∈Z  hoặc x=−a∘+k360∘,k∈Z. 

4. Phương trình tanx = m

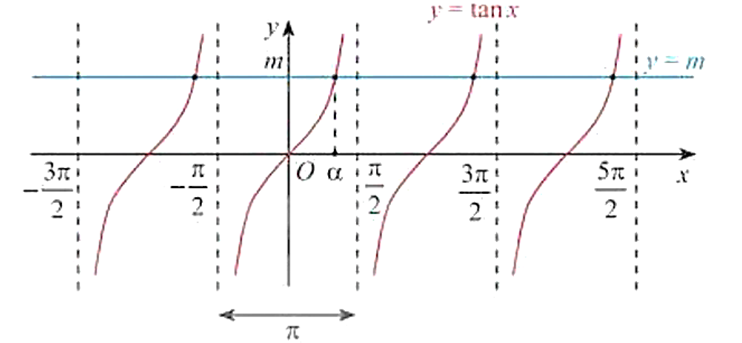
Với mọi số thực m, phương trình tanx=m  có nghiệm x=α+kπ,k∈Z, với α  là góc thuộc (−2π​;2π​)  sao cho tan α=m.

Chú ý: tanx=tana∘⇔x=a∘+k180∘,k∈Z. 

5. Phương trình cotx = m

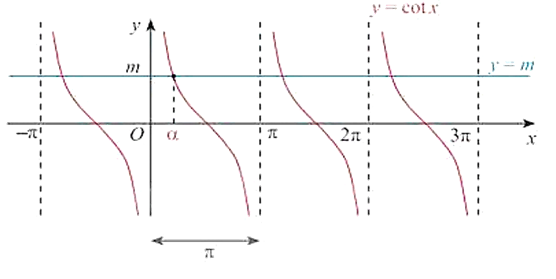
Với mọi số thực m , phương trình cotx=m  có nghiệm x=α+kπ,k∈Z, với α là góc thuộc (0;π)  sao cho cotα=m. 

Chú ý: cotx=cota∘⇔x=a0+k180∘,k∈Z. 

6. Giải phương trình lượng giác bằng máy tính cầm tay

• Ta có thể giải phương trình lượng giác dạng sinx=m,cosx=m,tanx=m  và cotx=m  bằng máy tính cầm tay như trong ví dụ sau:

Ví dụ 6. Sử dụng máy tính cầm tay để giải các phương trình sau:

a) sinx=−21​ . Kết quả ghi theo đơn vị radian.

b) cotx=3. Kết quả ghi theo đơn vị độ.

Lời giải

a) Chọn đơn vị đo góc là radian.

• Ấn liên tiếp các phím

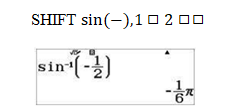
ta được một góc có sin  bằng −21​  là −6π​. 

Do đó, ta có các nghiệm của phương trình sinx=−21​  là

x=−6π​+k2π,k∈Z   v aˋ   x=67π​+k2π,k∈Z.    

b) Chọn đơn vị đo góc là độ.

• Ấn liên tiếp các phím

ta được một góc có côtang bằng 3 là 18,43∘ (làm tròn đến hàng phần trăm). 

• Do đó, ta có các nghiệm của phương trình cotx=3 là

x≈18,43∘+k180∘,k∈Z. 

Chú ý: Để giải phương trình cot x=m(m=0) , ta giải phương trình tanx=m1​.