1. Bài giảng: Phương trình mặt cầu trong không gian
Phương trình mặt cầu trong không gian
1. Định nghĩa
Trong không gian, tập hợp tất cả các điểm M cách điểm I cố định một khoảng không đổi là R(R>0) cho trước được gọi là mặt cầu tâm I bán kính R. Kí hiệu là S(I;R) hay viết tắt là (S).
Vậy S(I;R)={M∣IM=R}
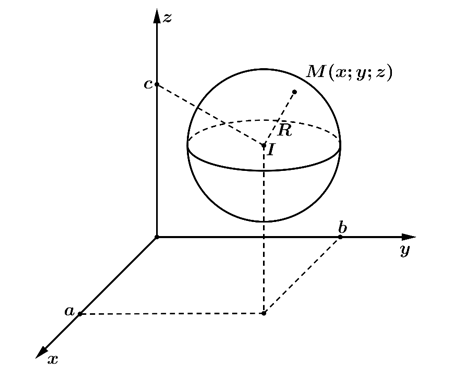
- Điểm M(x;y;z) nằm trong mặt cầu (S) nếu (x−a)2+(x−b)2+(x−c)2<R2.
- Điểm M(x;y;z) nằm trên mặt cầu (S) nếu (x−a)2+(x−b)2+(x−c)2=R2.
- Điểm M(x;y;z) nằm ngoài mặt cầu (S) nếu (x−a)2+(x−b)2+(x−c)2>R2.
2. Phương trình mặt cầu
Trong không gian Oxyz, cho mặt cầu (S) tâm I(a;b;c) bán kính R.
Phương trình mặt cầu (S) là: (x−a)2+(x−b)2+(x−c)2=R2.
Phương trình mặt cầu dạng khai triển là x2+y2+z2−2ax−2by−2cz+d=0 với a2+b2+c2−d>0 là phương trình của mặt cầu tâm I(a;b;c) và bán kính R=√a2+b2+c2−d.
2. Ví dụ minh hoạ: Phương trình mặt cầu trong không gian
Ví dụ 1:
Trong không gian Oxyz , cho mặt cầu (S):x2+y2+z2−12x−14y+10z+87=0 .
Tính bán kính mặt cầu (S) .
Lời giải:
Mặt cầu (S) có bán kính là: R=√62+72+(−5)2−87=√23 .
Ví dụ 2:
Trong không gian Oxyz , cho mặt cầu (S):x2+y2+z2−10x+16y+16z+151=0 .
Tọa độ tâm I của mặt cầu (S) là
Lời giải:
Mặt cầu (S) có tọa độ tâm là: I(5;−8;−8) .
3. Luyện tập củng cố: Phương trình mặt cầu trong không gian
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay