1. Bài giảng: Phương trình đường thẳng trong không gian
PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN
1. Vectơ chỉ phương của đường thẳng
Vectơ chỉ phương của đường phẳng: Vectơ u⃗=0⃗ được gọi là vectơ chỉ phương của đường thẳng Δ nếu giá của u⃗ song song hoặc trùng với Δ.
- Đường thẳng hoàn toàn xác định khi biết một điểm mà nó đi qua và một vectơ chỉ phương
- Nếu u⃗ là một vectơ chỉ phương của Δ thì k.u⃗ (với k là một số khác 0 ) cũng là một vectơ chỉ phương của Δ.
2. Phương trình tham số của đường thẳng
Định nghĩa: Trong không gian Oxyz, cho đường thẳng Δ đi qua điểm A(x0;y0;z0) và có vectơ chỉ phương u⃗=(a;b;c).
Hệ phương trình ⎩⎪⎨⎪⎧x=x0+aty=y0+btz=z0+ct được gọi là phương trình tham số của đường thẳng Δ (t là tham số, t∈R ).
Cho mặt phẳng (α) có phương trình tổng quát là Ax+By+Cz+D=0. Khi đó:
- Với các số a,b,c không đồng thời bằng 0 thì hệ phương trình ⎩⎪⎨⎪⎧x=x0+aty=y0+btz=z0+ct(t∈R) xác định một đường thẳng đi qua M(x0;y0;z0) và có vectơ chỉ phương là u⃗=(a;b;c).
- Từ phương trình tham số của đường thẳng, mỗi giá trị của tham số tương ứng với một điểm thuộc đường thẳng đó và ngược lại.
3. Phương trình chính tắc của đường thẳng
Trong không gian Oxyz, cho đường thẳng Δ đi qua điểm A(x0;y0;z0) và có vectơ chỉ phương u⃗=(a;b;c) với a,b,c là các số khác 0.
Hệ phương trình: ax−x0=by−y0=cz−z0 được gọi là phương trình chính tắc của đường thẳng Δ.
4. Lập phương trình đường thẳng đi qua hai điểm
- Trong không Oxyz, cho hai điểm phân biệt A1(x1;y1;z1) và A2(x2;y2;z2). Đường thẳng A1A2 có vectơ chỉ phương A1A2=(x2−x1;y2−y1;z2−z1).
- Đường thẳng A1A2 có phương trình tham số là ⎩⎪⎨⎪⎧x=x1+(x2−x1)ty=y1+(y2−y1)tz=z1+(z2−z1)t(t∈R).
- Trong trường hợp x1=x2 , y1=y2 , z1=z2 thì đường thẳng A1A2 có phương trình chính tắc là: x2−x1x−x1=y2−y1y−y1=z2−z1z−z1.
Trong không gian Oxyz, cho hai đường thẳng Δ1,Δ2 tương ứng có các vectơ chỉ phương u⃗1=(a1;b1;c1),u⃗2=(a2;b2;c2). Khi đó Δ1⊥Δ2⇔u⃗1.u⃗2=0⇔a1a2+b1b2+c1c2=0.
5. Vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz cho hai đường thẳng Δ1 , Δ2 lần lượt đi qua các điểm A1(x1;y1;z1) ,A2(x2;y2;z2) và tương ứng có vectơ chỉ phương u⃗1=(a1;b1;c1) , u⃗2=(a2;b2;c2) . Khi đó:
- Δ1∥Δ2⇔u⃗1 cùng phương với u⃗2 và A1∉Δ2.
- Δ1≡Δ2⇔u⃗1 cùng phương với u⃗2 và A1∈Δ2.
- Δ1 và Δ2 cắt nhau ⇔⎩⎨⎧[u⃗1,u⃗2]=0⃗A1A2⊥[u⃗1,u⃗2]⇔⎩⎨⎧[u⃗1,u⃗2]=0⃗A1A2⋅[u⃗1,u⃗2]=0.
- Δ1 và Δ2 chéo nhau ⇔A1A2.[u⃗1,u⃗2]=0.
Trong không gian Oxyz, cho hai đường thẳng Δ1 , Δ2 tương ứng có vectơ chỉ phương lần lượt là u⃗1=(a1;b1;c1) , u⃗2=(a2;b2;c2) và có phương trình tham số: Δ1:⎩⎪⎨⎪⎧x=x1+a1ty=y1+b1tz=z1+c1tΔ2:⎩⎪⎨⎪⎧x=x2+a2ty=y2+b2tz=z2+c2t
Xét hệ phương trình hai ẩn t và s : ⎩⎪⎨⎪⎧x1+a1t=x2+a2sy1+b1t=y2+b2sz1+c1t=z2+c2s(∗). Khi đó
- Δ1∥Δ2⇔u⃗1 cùng phương với u⃗2 và hệ (∗) vô nghiệm.
- Δ1≡Δ2⇔ Hệ (∗) có vô số nghiệm.
- Δ1 cắt Δ2⇔ Hệ (∗) có nghiệm duy nhất.
- Δ1 và Δ2 chéo nhau ⇔u⃗1 và u⃗2 không cùng phương và hệ (∗) vô nghiệm.
6. Góc
Góc giữa hai đường thẳng:
Trong không gian Oxyz, cho hai đường thẳng Δ1,Δ2 tương ứng có u⃗1=(a1;b1;c1) và u⃗2=(a2;b2;c2) là hai vectơ chỉ phương. Khi đó, ta có:
cos(Δ1,Δ2)=∣cos(u⃗1.u⃗2)∣=∣u⃗1∣.∣u⃗2∣∣u⃗1.u⃗2∣=√a12+b12+c12.√a22+b22+c22∣a1a2+b1b2+c1c2∣
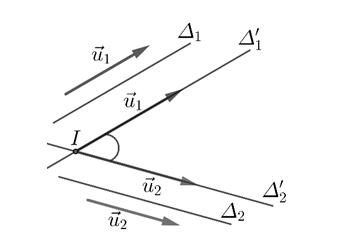
Góc giữa đường thẳng và mặt phẳng:
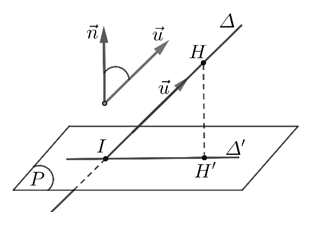
Trong không gian Oxyz, cho đường thẳng Δ có vectơ chỉ phương u⃗=(a;b;c) và mặt phẳng (P) có vectơ pháp tuyến n⃗=(A;B;C) . Khi đó, ta có:
sin(Δ,(P))=∣cos(u⃗.n⃗)∣=∣u⃗∣.∣n⃗∣∣u⃗.n⃗∣=√a2+b2+c2.√A2+B2+C2∣aA+bB+cC∣
Góc giữa hai mặt phẳng:
Trong không gian Oxyz, cho hai mặt phẳng (P1),(P2) có hai vectơ pháp tuyến lần lượt làn⃗1=(A1;B1;C1) và n⃗2=(A2;B2;C2). Khi đó, ta có:
cos((P1),(P2))=∣cos(n⃗1.n⃗2)∣ =∣n⃗1∣.∣n⃗22∣∣n⃗1.n⃗2∣=√A12+B12+C12.√A22+B22+C22∣A1A2+B1B2+C1C2∣
2. Ví dụ minh hoạ: Phương trình đường thẳng trong không gian
Ví dụ 1:
Trong không gian Oxyz , cho đường thẳng d:⎩⎨⎧x=8+2ty=7+2tz=−6+3t Đường thẳng d đi qua điểm nào trong các điểm sau?
Lời giải:
Tồn tại t=1⇒x=10,y=9,z=−3 nên đường thẳng d đi qua C=(10;9;−3) .
Ví dụ 2:
Trong không gian Oxyz , cho đường thẳngΔ:⎩⎨⎧x=−4−7ty=−1−4tz=5−8t Đường thẳng Δ đi qua điểm nào trong các điểm sau?
Lời giải:
Tồn tại t=1⇒x=−11,y=−5,z=−3 nên đường thẳng Δ đi qua A=(−11;−5;−3) .
3. Luyện tập củng cố: Phương trình đường thẳng trong không gian
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay