1. Bài giảng: Phương trình mặt phẳng
P
HƯƠNG TRÌNH MẶT PHẲNG
1. Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng
Vectơ pháp tuyến của mặt phẳng: Cho mặt phẳng (α). Vectơ n⃗=0⃗ và có giá vuông góc với mặt phẳng (α) gọi là vectơ pháp tuyến của mặt phẳng (α).
- Nếu n⃗ là một vectơ pháp tuyến của (α) thì k.n⃗ (k=0) cũng là một vectơ pháp tuyến của (α).
- Một mặt phẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của nó.
Cặp vectơ chỉ phương của mặt phẳng: Cho mặt phẳng (α). Nếu hai vectơ a⃗ và b⃗ không cùng phương và giá của chúng song song hoặc nằm trên mặt phẳng(α) thì a⃗,b⃗ là cặp véctơ chỉ phương của mặt phẳng (α).
Một mặt phẳng hoàn toàn được xác định khi biết một điểm và cặp vectơ chỉ phương của nó.
Vectơ pháp tuyến của mặt phẳng khi biết một cặp vectơ chỉ phương : Trong không gian Oxyz, nếu mặt phẳng (α) nhận hai vectơ a⃗=(a1;a2;a3) và b⃗=(b1;b2;b3) làm cặp vectơ chỉ phương thì (α) nhận n⃗=[a⃗,b⃗] làm vectơ pháp tuyến.
Vectơ n⃗=(a2b3−a3b2;a3b1−a1b3;a1b2−a2b1) được gọi là tích có hướng của hai vectơ a⃗=(a1;a2;a3) và b⃗=(b1;b2;b3). Tích có hướng của hai vectơ a⃗ và b⃗ được kí hiệu là [a⃗,b⃗].
- [a⃗,b⃗]=(∣∣∣∣∣a2 a3b2 b3∣∣∣∣∣;∣∣∣∣∣a3 a1 b3 b1∣∣∣∣∣;∣∣∣∣∣a1 a2b1 b2∣∣∣∣∣)=(a2b3−a3b2;a3b1−a1b3;a1b2−a2b1).
- a⃗ cùng phương với b⃗ ⇔[a⃗,b⃗]=0⃗.
- Nếu n⃗=[a⃗,b⃗]thì vectơ n⃗ vuông góc với cả hai vectơ a⃗ và b⃗.
2. Phương trình tổng quát của mặt phẳng
Định nghĩa: Trong không gian Oxyz, phương trình có dạng Ax+By+Cz+D=0, trong đó A,B,C không đồng thời bằng 0 được gọi là phương trình tổng quát của mặt phẳng.
Nhận xét: Cho mặt phẳng (α) có phương trình tổng quát là Ax+By+Cz+D=0. Khi đó:
- Mặt phẳng (α) có một vec-tơ pháp tuyến là n⃗=(A;B;C)
- Điểm N(x0;y0;z0)∈(α)⇔Ax0+By0+Cz0+D=0
- Mỗi phương trình Ax+By+Cz+D=0 (trong đó A,B,C không đồng thời bằng 0) đều là phương trình của một mặt phẳng xác định.
Một số dạng toán viết phương trình mặt phẳng cơ bản:
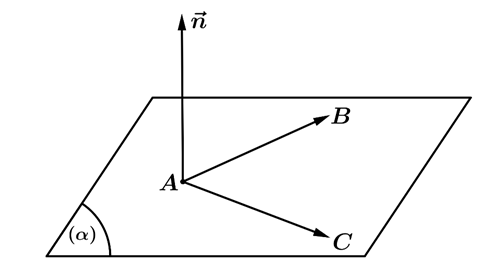
Dạng 1: Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một vectơ pháp tuyến

Trong không gian Oxyz, phương trình mặt phẳng đi qua điểm M0(x0;y0;z0) và có một vectơ pháp tuyến n⃗=(A;B;C) là: A(x−x0)+B(y−y0)+C(z−z0)=0 ⇔Ax+By+Cz+D=0 với D=−Ax0−By0−Cz0.
Dạng 2: Lập phương trình tổng quát của mặt phẳng đi qua một điểm và có một cặp vectơ chỉ phương
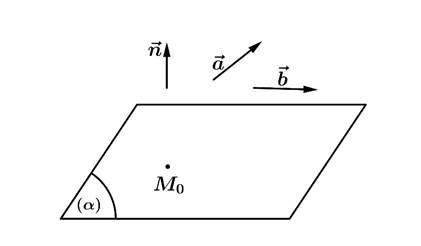
Để lập phương trình tổng quát của mặt phẳng (α) đi qua điểm M0(x0;y0;z0) và có cặp vectơ chỉ phương a⃗ , b⃗ thì ta thực hiện như sau:
Bước 1: Tìm một vectơ pháp tuyến n⃗=[a⃗,b⃗].
Bước 2: Viết phương trình mặt phẳng (α) đi qua điểm M0(x0;y0;z0) và có vectơ pháp tuyến n⃗.
Dạng 3: Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng Để lập phương trình tổng quát của mặt phẳng (α) đi qua ba điểm A,B,C không thẳng hàng thì ta thực hiện như sau:
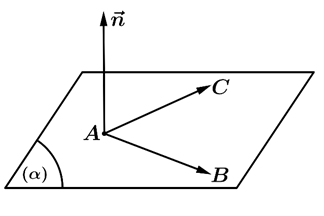
Bước 1: Tìm cặp vectơ chỉ phương chẳng hạn AB,AC.
Bước 2: Tìm một vectơ pháp tuyến n⃗=[AB,AC].
Bước 3: Viết phương trình mặt phẳng (α) đi qua A và có vectơ pháp tuyến n⃗.
Dạng 4: Lập phương trình tổng quát của mặt phẳng theo đoạn chắn
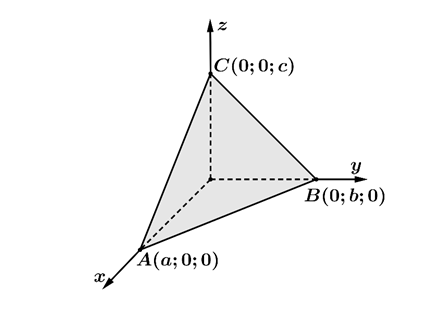
Phương trình tổng quát của mặt phẳng (α) đi qua ba điểm A(a;0;0),B(0;b;0),C(0;0;c) là:
ax+by+cz=1.
3. Điều kiện để hai mặt phẳng song song hoặc vuông góc.
Điều kiện để hai mặt phẳng song song: Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng có phương trình lần lượt là (α1):A1x+B1y+C1z+D1=0 và (α2):A2x+B2y+C2z+D2=0 có vectơ pháp tuyến lần lượt là n⃗1=(A1;B1;C1),n⃗2=(A2;B2;C2). Khi đó: (α1)∥(α2)⇔{n⃗1=kn⃗2D1=kD2(k∈R).
Ta có một số tính chất sau:
- (α1)≡(α2)⇔{n⃗1=kn⃗2D1=kD2(k∈R).
- (α1) cắt (α2)⇔n⃗1 và n⃗2 không cùng phương.
Điều kiện để hai mặt phẳng vuông góc: Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng có phương trình lần lượt là (α1):A1x+B1y+C1z+D1=0 và (α2):A2x+B2y+C2z+D2=0 có vectơ pháp tuyến lần lượt là n⃗1=(A1;B1;C1),n⃗2=(A2;B2;C2).
Khi đó: (α1)⊥(α2)⇔n⃗1.n⃗2=0⇔A1A2+B1B2+C1C2=0.
4. Khoảng cách từ một điểm đến một mặt phẳng
Trong không gian Oxyz, mặt phẳng (α) có phương trình Ax+By+Cz+D=0 và điểm M0(x0;y0;z0). Khoảng cách từ điểm M0 đến mặt phẳng (α) được tính theo công thức:
d(M0,(α))=√A2+B2+C2∣Ax0+By0+Cz0+D∣.
5. Các phương trình mặt phẳng đặc biệt trong không gian
| Tính chất mặt phẳng | Phương trình | Hệ số đặc biệt |
|
(α) đi qua/chứa gốc O |
(α):Ax+By+Cz=0 |
D=0 |
|
(α) song song/chứa Ox |
(α):By+Cz+D=0 |
A=0 |
|
(α) song song/chứa Oy |
(α):Ax+Cz+D=0 |
B=0 |
|
(α) song song/chứa Oz |
(α):Ax+By+D=0 |
C=0 |
|
(α) song song/trùng (Oxy) |
(α):Cz+D=0 |
A=B=0 |
|
(α) song song/trùng (Oxz) |
(α):By+D=0 |
A=C=0 |
|
(α) song song/trùng (Oyz) |
(α):Ax+D=0 |
B=C=0 |
Mặt phẳng không chứa ẩn nào thì mặt phẳng sẽ song song/chứa trục đó hoặc mặt phẳng không chứa ẩn nào thì mặt phẳng sẽ song song/chứa mặt phẳng đó.
2. Ví dụ minh hoạ: Phương trình mặt phẳng
Ví dụ 1:
Trong không gian Oxyz , cho mặt phẳng (Q) có phương trình −4x+3y+z+16=0 . Mặt phẳng (Q) nhận vectơ nào trong các vectơ sau làm véctơ pháp tuyến.
Lời giải:
Mặt phẳng (Q) có một véctơ pháp tuyến là n⃗=(−4;3;1) .
Ví dụ 2:
Trong không gian với hệ tọa độ Oxyz , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (Oxy) ?
Lời giải:
k⃗=(0;0;1)
3. Luyện tập củng cố: Phương trình mặt phẳng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay