1. Bài giảng: Ứng dụng của tích phân vào bài toán thể tích
Ứng dụng tích phân vào bài toán thể tích
Phương pháp:
Thể tích vật thể tính theo mặt cắt vuông góc trục hoành
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b, S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a≤x≤b)
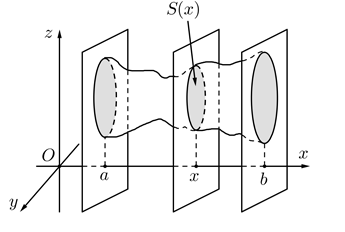
Giả sử S(x) là hàm số liên tục trên đoạn [a;b]
Khi đó, thể tích của vật thể B được xác định: V=a∫bS(x)dx
Thể tích khối tròn xoay
Xoay miền hình phẳng giới hạn: {y=f(x)Ox;x=a;x=b quanh trục Ox.
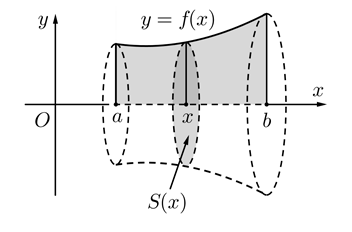
Bước 1: Giải f(x)=0⇔x=c;c∈[a;b].
Bước 2: Tính V=πa∫b(f(x))2dx
2. Ví dụ minh hoạ: Ứng dụng của tích phân vào bài toán thể tích
Ví dụ 1:
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ).
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−1≤x≤1) thì được thiết diện là một tam giác đều.
Tính thể tích V của vật thể đó.

Lời giải:
Tại vị trí có hoành độ x (−1≤x≤1) thì tam giác thiết diện có cạnh là 2√1−x2 .
Do đó tam giác thiết diện có diện tích S(x)=(2√1−x2)24√3 =√3(1−x2) .
Vậy thể tích V của vật thể là −1∫1√3(1−x2)dx =34√3 .
Ví dụ 2:
Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình x2+y2=1 và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình vẽ bên).

Lời giải:
+) Ta có x2+y2=1 ⇔y=±√1−x2 , với −1≤x≤1 .
+) Vật thể (T) cần tính thể tích được giới hạn bởi mặt phẳng (α):x=−1 và (β):x=1 .
+) Cắt vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x , x∈[0;1] ta được thiết diện là hình vuông cạnh AB=2√1−x2 .
Diện tích thiết diện là S(x)=AB2=4(1−x2) .
Thể tích vật thể là: V=−1∫1S(x)dx =−1∫14(1−x2)dx =4(x−31x3)∣∣∣−11=316 .
Vậy V=316(dvtt) .
3. Luyện tập củng cố: Ứng dụng của tích phân vào bài toán thể tích
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay