1. Bài giảng: Phương trình, bất phương trình mũ và lôgarit
Phương trình, Bất phương trình Mũ - Loga
1. Phương trình
1.1. PHƯƠNG TRÌNH MŨ
- Phương trình mũ cơ bản có dạng: ax=b (a>0, a=1).
- Phương trình có một nghiệm duy nhất khi và chỉ khi b>0.
- ax=b⇔x=logab (a>0, a=1,b>0)
- Phương trình vô nghiệm khi và chỉ khi b≤0.
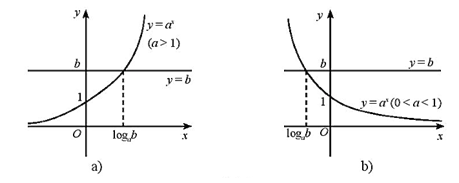
- Cho phương trình ax=b(a>0,a=1).
- Nếu b>0 thì phương trình luôn có nghiệm duy nhất x=logab.
- Nếu b≤0 thì phương trình vô nghiệm.
a) Nếu b=aα thi ta có ax=aα⇔x=α.
b) Tổng quát hơn, d ′ (x)=aı(x)⇔u(x)=v(x).
1.2. PHƯƠNG TRÌNH LÔGARIT
- Phương trình cơ bản có dạng: logax=b(x>0,a>0,a=1) luôn có nghiệm duy nhất x=ab với mọi b
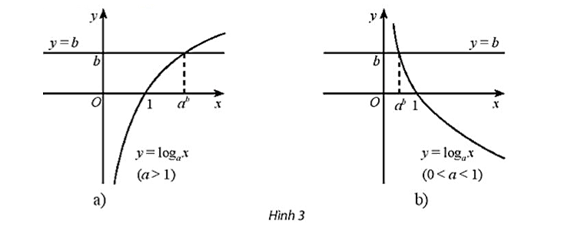
Tổng quát, xét phương trình dạng
- logau(x)=logav(x) (a>0,a=1)
- Để giải phương trình (1), trước hết cần đặt điều kiện có nghĩa: u(x)>0 và v(x)>0.
- Khi đó, (1) được biến đổi thành phương trình u(x)=v(x)
- Sau khi giải phương trình (2), ta cần kiểm tra sự thoả mãn điều kiện. Nghiệm của phương trình (1) là những nghiệm của (2) thoả mãn điều kiện.
1.3. BẤT PHƯƠNG TRÌNH MŨ
- Bất phương trình mũ cơ bản là bất phương trình có dạng ax>b (hoặc ax≥b,ax<b , ax≤b ), với a,b là những số cho trước, a>0,a=1.
- Xét bất phương trình ax>b
- Nghiệm của (3) là hoành độ các điểm trên đồ thị hàm số y=ax nằm phía trên đường thẳng y=b . Từ đồ thị ở Hình 4 , ta nhận được:
+ Nếu b≤0 thì mọi x∈R đều là nghiệm của (3).
+ Nếu b>0 thì:
+ Với a>1 , nghiệm của (3) là x>logab,
+ Với 0<a<1 , nghiệm của (3) là x<logab.
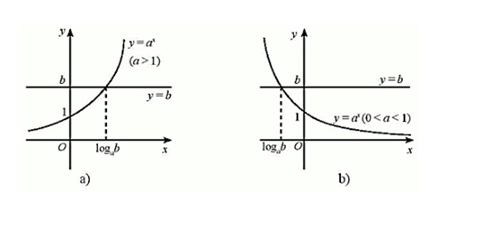
- Nếu a>1 , b>0 thì af(x)>ag(x)⇔f(x)>g(x)
- af(x)>b⇔f(x)>logab
- Nếu 0<a<1 , b>0 thì af(x)>ag(x)⇔f(x)<g(x)
- af(x)>b⇔f(x)<logab
b≤0 thì af(x)>b đúng với mọi x thỏa mãn điều kiện xác định củaf(x), còn af(x)≤b vô nghiệm.
1.4 BẤT PHƯƠNG TRÌNH LOGARIT
- Bất phương trình lôgarit cơ bản là bất phương trình có dạng logαx>b (hoặc logαx≥b , logax<b,logax≤b ), với a,b là những số cho trước, a>0,a=1.
- Xét bất phương trình logαx>b
- Điều kiện xác định của bất phương trình là x>0.
- Nghiệm của (4) là hoành độ các điểm của đồ thị hàm số y=logax nằm phía trên đường thẳng y=b. Từ đồ thị ở Hình 5, ta nhận được:
- Với a>1, nghiệm của (4) là x>ab.
- Với 0<a<1 , nghiệm của (4) là 0<x<ab.
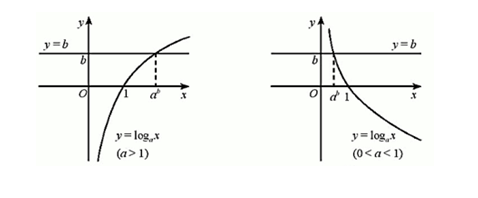
- Nếu a>1 thì logaf(x)>logag(x)⇔{g(x)>0f(x)>g(x)
- Nếu 0<a<1 thì logaf(x)>logag(x)⇔{f(x)>0f(x)<g(x)
2. Ví dụ minh hoạ: Phương trình, bất phương trình mũ và lôgarit
Ví dụ 1:
Cho phương trình 3x2−4x+5=9 tổng lập phương các nghiệm thực của phương trình là:
Lời giải:
Ta có: 3x2−4x+5=9⇔3x2−4x+5=32⇔x2−4x+5=2⇔x2−4x+3=0⇔[x=1x=3
Suy ra 13+33=28 .
Ví dụ 2:
Cho phương trình: 3x2−3x+8=92x−1 , khi đó tập nghiệm của phương trình là:
Lời giải:
Ta có:
3x2−3x+8=92x−1⇔3x2−3x+8=34x−2⇔x2−3x+8=4x−2⇔x2−7x+10=0⇔[x=5x=2
3. Luyện tập củng cố: Phương trình, bất phương trình mũ và lôgarit
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay