logo

1. Bài giảng: Hàm số mũ và hàm số lôgarit

Hàm số mũ - Hàm số logarit

Hàm số mũ Hàm số logarit
Định nghĩa

Hàm số y=ax,(a>0,a=1)  được gọi là hàm số mũ cơ số a. 

Hàm số y=loga​x,(a>0,a=1)  được gọi là hàm số lôgarit cơ số a. 
Tập xác định

D=R 

D=(0;+∞) 
Tập giá trị

T=(0;+∞) 

T=R 
Tính đơn điệu

Khi a>1: Hàm số y=ax  đồng biến trên R; x→−∞lim​ax=0;x→+∞lim​ax=+∞

Khi 0<a<1: Hàm số y=ax nghịch biến trên R; x→−∞lim​ax=+∞;x→+∞lim​ax=0 

Đồ thị :

  • Đi qua điểm (0;1) và (1;a).

  • Liên tục trên R. 

  • Nằm ở phía trên trục hoành.

Đồ thị:

  • Đi qua điểm (1;0) và

  • Liên tục trên (0;+∞).

  • Nằm ở bên phải trục tung.

     
Đồ thị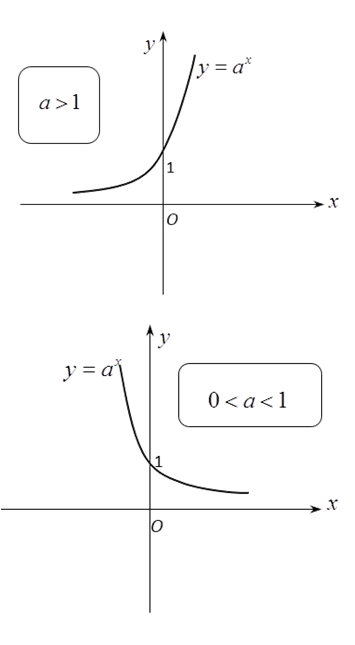

 

2. Ví dụ minh hoạ: Hàm số mũ và hàm số lôgarit

Ví dụ 1:

Tập xác định của hàm số y=log2​2−xx+3​  là:

Câu trả lời

  • D=(−3;2)  

  • D=R\ { −3;2}  

  • D=(−∞;−3)∪(2;+∞)  

  • D= [ −3;2] 

Lời giải:

Hàm số log2​2−xx+3​  có nghĩa khi 2−xx+3​>0⇔−3<x<2  .

Ví dụ 2:

Tìm tập xác định D của hàm sốy=log3​x2−3x+210−x​ .

Câu trả lời

  • D=(−∞;1)∪(2;10)  

  • D=(1;+∞)  

  • D=(−∞;10)  

  • D=(2;10) 

Lời giải:

Hàm số xác định ⇔x2−3x+210−x​>0⇔x<1 hoặc 2<x<10  Tập xác định D=(−∞;1)∪(2;10) 

3. Luyện tập củng cố: Hàm số mũ và hàm số lôgarit

Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái

Luyện tập ngay

4. Các đơn vị kiến thức cùng chuyên đề