Góc và tích vô hướng của 2 vector

1. Định nghĩa góc giữa hai vectơ

• Cho hai vectơ u  và v  khác vectơ 0. Từ một điểm A tuỳ ý, vẽ các vec tơ AB=u  và AC=v  Khi đó số đo của góc BAC được gọi là số đo của góc giữa hai vectơ u⃗,v⃗ , kí hiệu là (u⃗,v⃗). 

Chú ý:
+ Quy ước rằng góc giữa hai vectơ u⃗  và 0⃗ có thể nhận một giá trị tuỳ ý từ 0∘ đến 180∘. 
+ Nếu (u⃗,v⃗)=90∘ thì ta nói rằng u và v vuông góc với nhau, kí hiệu là u⊥v⃗  hoặc v⊥u⃗. 
+ Đặc biệt vectơ 0⃗ được coi là vuông góc với mọi vectơ.

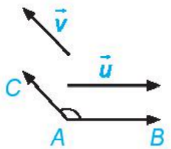
2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không u  và v  là một số, kí hiệu là u.v  được xác định bởi công thức sau: u⃗.v⃗=∣u⃗∣.∣v⃗∣.cos(u⃗,v⃗). 

Chú ý:
+ u⊥v⇔u.v=0.  hoặc v⊥u⃗.  Tíchu.u  còn được viết là u2  và được gọi là bình phương vô hướng của u.+  Ta có u⃗2=∣u⃗∣.∣u⃗∣.cos0∘=∣u⃗∣2. 
+ Tích vô hướng của hai vectơ u⃗(x;y) và v⃗(x′;y′)  được tính theo công thức: u⃗.v⃗=x.x′+u.u′ 

3. Biểu thức toạ độ và tính chất của tích vô hướng

• Tích vô hướng của hai vectơ u⃗(x;y) và v⃗(x′;y′)  được tính theo công thức:

u⃗.v⃗=x.x′+u.u′ 

Nhận xét

• Hai vectơ u⃗  và v⃗ vuông góc với nhau khi và chỉ khi x.x′+y.y′=0.  Bình phương vô hướng của vectơ u⃗(x;y) là u⃗2=x2+y2. 
• Nếu u⃗=0⃗  và v⃗=0⃗  thì cos(u⃗,v⃗)=∣u⃗∣.∣v⃗∣u⃗.v⃗​=√x2+y2​.√x′2+y′2​xx′+yy′​. 

Tính chất

• Với ba vectơ u, v, w bất kì và mọi số thực k ta có: u.v=v.u  ( tính chất giao hoán);
• u.(v+w)=u.v+u.w  ( Tính chất phân phối đối với phép cộng);
• (ku).v=k(u.v)=u.(kv).