1. Bài giảng: Tọa độ vector và các phép toán vetor trong mặt phẳng tọa độ
TỌA ĐỘ VECTOR VÀ CÁC PHÉP TOÁN VETOR TRONG MẶT PHẲNG TỌA ĐỘ
1. Trục và độ dài đại số trên trục
- Trục toạ độ (O;e⃗)
- Toạ độ của điểm trên trục: Cho M trên trục (O;e⃗)
![]()
- k là toạ độ của OM=ke⃗
- Độ dài đại số của vectơ: Cho A,B trên trục (O;e⃗ ).
- a=AB⇔AB=ae⃗
![]()
- AB cùng hướng e⃗⇔AB>0
- AB ngược hướng e⃗⇔AB<0
- Nếu A(a),B(b) thì AB=b−a
- AB=∣∣∣∣AB∣∣∣∣=∣∣AB∣∣=∣b−a∣
- Nếu A(a),B(b),I là trung điểm của AB thì I(2a+b)
- Nếu AB cùng hướng với i thì AB=AB, còn nếu AB ngược hướng với i thì AB=−AB.
- Nếu hai điểm A và B trên trục (O;i) có tọa độ lần lượt là a và b thì AB=b−a.
2. Hệ trục toạ độ
- Hệ trục toạ độ (O;i⃗;j⃗)
- gốc toạ độ
- Trục (O;i⃗): trục hoành Ox
- Trục (O;j⃗): trục tung Oy
- i⃗,j⃗ là các vectơ đơn vị
- Hệ (O;i⃗;j⃗) còn kí hiệu Oxy
- Mặt phẳng toạ độ Oxy.
1. Toạ độ của vectơ
- u⃗=(x;y)⇔u⃗=xi⃗+yj⃗
- Cho u⃗=(x;y),u⃗′=(x′;y′)
- u⃗=u⃗′⇔{x=x′y=y′
- Mỗi vectơ được hoàn toàn xác định khi biết toạ độ của nó
- i⃗=(1;0),j⃗=(0;1)
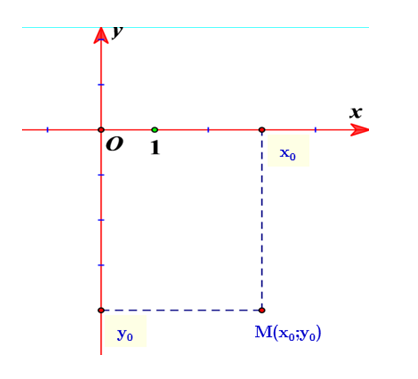
2. Toạ độ của điểm
- M(x;y)⇔OM=(x;y)
- Nếu MM1⊥Ox,MM2⊥Oy thì x=OM1,y=OM2
- Nếu M∈Ox thì yM=0
- M∈Oy thì xM=0
- Độ dài của OM là OM=∣∣∣∣OM∣∣∣∣=√x2+y2
3. Liên hệ giữa toạ độ của điểm và vectơ trong mặt phẳng
- Cho A(xA;yA),B(xB;yB).
- AB=(xB−xA;yB−yA)
- AB=∣∣∣∣AB∣∣∣∣=√(xB−xA)2+(yB−yA)2
4. Tọa độ của các vectơ u⃗+v⃗,u⃗−v⃗,ku⃗:
- Cho u⃗=(u1;u2),v⃗=(v1;v2).
- u⃗+v⃗=(u1+v1;u2+v2)
- u⃗−v⃗=(u1−v1;u2−v2)
- ku⃗=(ku1;ku2),k∈R
Hai vectơ u⃗=(u1;u2),v⃗=(v1;v2) với v⃗=0⃗ cùng phương⇔∃k∈R sao cho: {u1=kv1u2=kv2
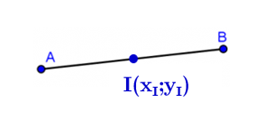
5. Toạ độ của trung điểm đoạn thẳng, của trọng tâm tam giác
- Cho A(xA;yA),B(xB;yB). I là trung điểm của AB thì:
xI=2xA+xB,yI=2yA+yB
- Cho ΔABC với A(xA;yA),B(xB;yB),C(xC;yC). G là trọng tâm của ΔABC thì:
⎩⎪⎨⎪⎧xG=3xA+xB+xCyG=3yA+yB+yC

2. Ví dụ minh hoạ: Tọa độ vector và các phép toán vetor trong mặt phẳng tọa độ
Ví dụ 1:
Trong hệ trục tọa độ (O;i;j) tọa độ v=5i−8j là:
Lời giải:
Ta có i=(1;0), j=(0;1)u=5i−8j=(5;−8).
Ví dụ 2:
Vecto nào là vecto đơn vị theo trục Ox
Lời giải:
i=(0;1)
3. Luyện tập củng cố: Tọa độ vector và các phép toán vetor trong mặt phẳng tọa độ
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay