1. Bài giảng: Sự đồng quy của ba đường cao trong một tam giác
SỰ ĐỒNG QUY CỦA BA ĐƯỜNG CAO TRONG MỘT TAM GIÁC
Tính chất ba đường cao của tam giác
a) Đường cao của tam giác

- Đoạn thẳng AI là một đường cao của ABC. Ta nói AI là đường cao xuất phát từ đỉnh A (hay đường cao ứng với cạnh BC).
b) Tính chất ba đường cao của tam giác
- Ba đường cao trong một tam giác đồng quy tại một điểm.
- Điểm đồng quy của ba đường cao trong một tam giác gọi là trực tâm của tam giác đó.
- Gọi H là trực tâm của tam giác ABC, ta có:
- Nếu tam giác ABC nhọn thì H nằm bên trong tam giác.
- Nếu tam giác ABC vuông tại A thì H trùng với A.
- Nếu tam giác ABC tù thì H nằm bên ngoài tam giác.
- Trong tam giác cân tại A, đường cao xuất phát từ đỉnh A đồng thời là đường trung trực, đường phân giác, đường trung tuyến của tam giác đó.
2. Ví dụ minh hoạ: Sự đồng quy của ba đường cao trong một tam giác
Ví dụ 1:
Ông Hùng có ba cửa hàng A, B, C không nằm trên một đường thẳng và đang muốn tìm địa điểm O để làm kho hàng. Phải chọn vị trí của kho hàng ở đâu để khoảng cách từ kho đến các cửa hàng bằng nhau?
Lời giải:
Ta có hình vẽ:

Vì điểm O cách đều ba điểm A, B, C nên O là giao của ba đường trung trực của tam giác ABC hay O là tâm đường tròn ngoại tiếp tam giác ABC.
Để xác định vị trí điểm O ta chỉ cần xác định giao điểm của hai trong ba đường trung trực của tam giác ABC.
Vậy kho hàng ở giao điểm của hai đường trung trực của AB và AC để khoảng cách từ kho đến các cửa hàng bằng nhau.
Ví dụ 2:
Ba thành phố A,B,C trên bản đồ là ba đỉnh của một tam giác đều có G là trọng tâm, biết GB=10 cm. Tính độ dài đường cao AH trên bản đồ
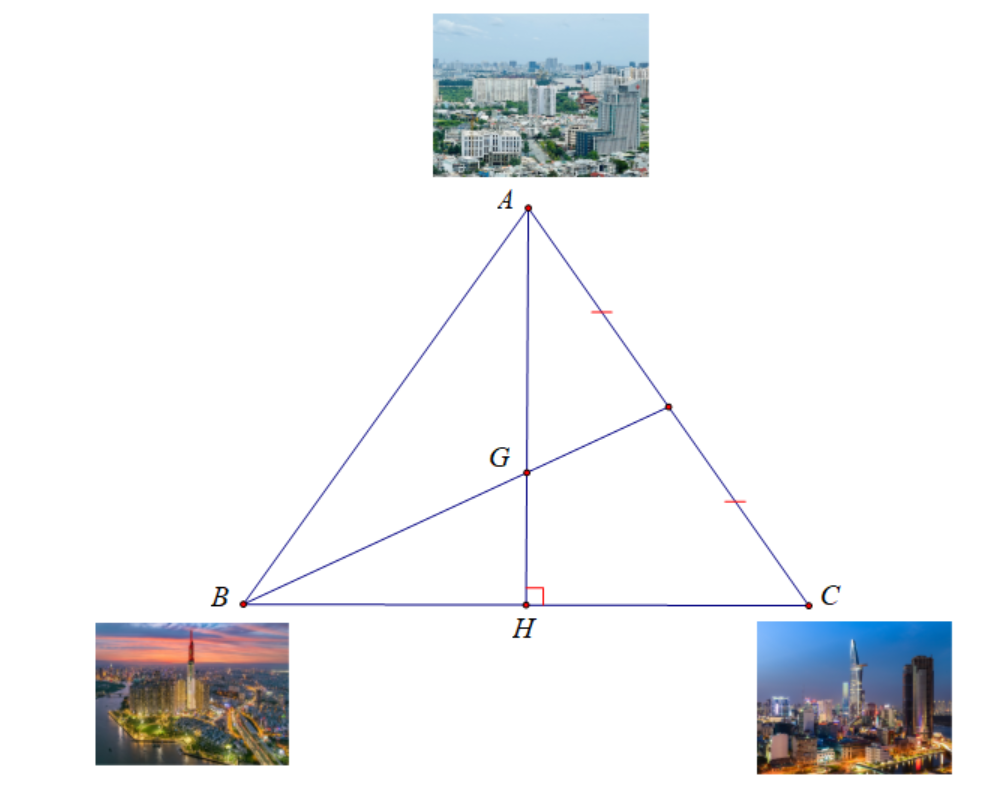
Lời giải:
Vì △ABC là tam giác đều có G là trọng tâm nên ta có GA=GB=10cm.
Ta lại có AH là đường trung tuyến của △ABC suy ra GA=32AH hay AH=23GA=23⋅10=15cm.
3. Luyện tập củng cố: Sự đồng quy của ba đường cao trong một tam giác
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay