1. Bài giảng: Các trường hợp bằng nhau của tam giác vuông
CÁC TRƯỜNG HỢP BẰNG NHAU CỦA TAM GIÁC VUÔNG
Các trường hợp bằng nhau của tam giác vuông
Trường hợp 1: Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Trường hợp 2: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Trường hợp 3: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Trường hợp đặc biệt: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

2. Ví dụ minh hoạ: Các trường hợp bằng nhau của tam giác vuông
Ví dụ 1:
Cho ∆ABC có AB=AC,AM là tia phân giác của A(M∈BC). Kẻ MD vuông góc AB tại D,ME vuông góc AC tại E. Tam giác ∆AMD bằng tam giác nào?
Lời giải:

Xét △AMD và △AME , có:
ADM=AEM=90∘ (MD⊥AB tại D,ME⊥AC tại E ).
AM là cạnh chung.
DAM=EAM (AM là tia phân giác của A ).
Do đó △AMD=△AME (cạnh huyền – góc nhọn).
Vậy △AMD=△AME .
Ví dụ 2:
Cho ∆MNP và ∆GHI có M=G=90° và NP=HI. Cần thêm điều kiện gì để ∆MNP=∆GHI theo trường hợp cạnh huyền – góc nhọn?
Lời giải:
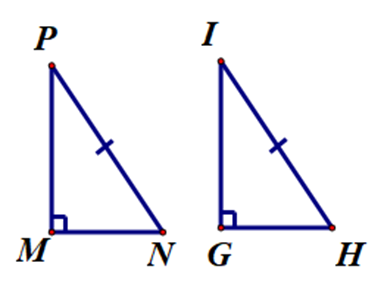
Bài toán cho sẵn: hai tam giác MNP và GHI có M=G=90° và NP=HI.
Ta thấy NP,HI lần lượt là cạnh huyền của △MNP và △GHI .
Do đó ta cần thêm điều kiện: góc nhọn của tam giác vuông này bằng góc nhọn tương ứng của tam giác vuông kia.
Ta thấy có thể xảy ra 2 trường hợp:
Trường hợp 1: N=H .
Trường hợp 2: P=I .
Do đó để △MNP=△GHI theo trường hợp cạnh huyền - góc nhọn, ta cần thêm điều kiện N=H hoặc P=I .
3. Luyện tập củng cố: Các trường hợp bằng nhau của tam giác vuông
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay