1. Bài giảng: Ứng dụng của tích phân vào bài toán diện tích
Ứng dụng của tích phân vào bài toán diện tích
1. Tính diện tích hình phẳng
Hình phẳng giới hạn bởi đồ thị của một hàm số, trục hoành và hai đường thẳng x=a,x=b
Ta đã biết, nếu hàm số y=f(x) liên tục và không âm trên đoạn [a;b] thì diện tích hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b được tính bởi:
S=a∫bf(x)dx
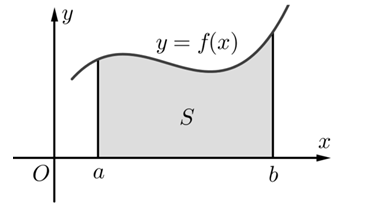
Một cách tổng quát, ta có kết quả sau:
Cho hàm số y=f(x) liên tục trên đoạn [a;b] . Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của hàm số y=f(x) , trục hoành và hai đường thẳng x=a,x=b được tính bởi công thức:
S=a∫b∣f(x)∣dx
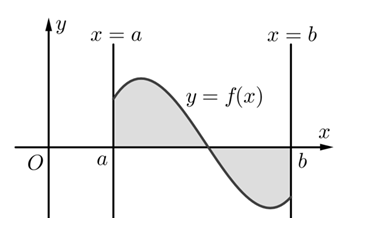
Giả sử hàm số y=f(x) liên tục trên đoạn [a;b] . Nếu f(x) không đổi dấu trên đoạn [a;b] thì:
a∫b∣f(x)∣dx=∣∣∣∣∣∣a∫bf(x)dx∣∣∣∣∣∣
Nếu phương trình f(x)=0 không có nghiệm trên khoảng (a;b) thì công thức trên vẫn đúng.
Hình phẳng giới hạn bởi đồ thị của hai hàm số và hai đường thẳng x=a,x=b
Cho hai hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b] . Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số trên và hai đường thẳng x=a,x=b . Xét trường hợp f(x)≥g(x) với mọi x∈[a;b] . Kí hiệu S1,S2 là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng x=a,x=b và đồ thị của hàm số y=f(x),y=g(x) tương ứng. Khi đó:
S=S1−S2=a∫bf(x)dx−a∫bg(x)dx=a∫b[f(x)−g(x)]dx
Trong trường hợp tổng quát, ta có kết quả sau:
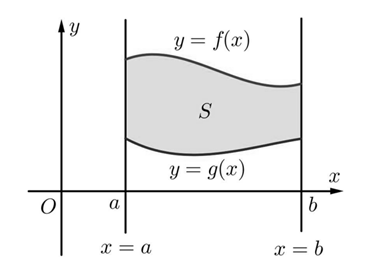
Cho hai hàm số y=f(x),y=g(x) liên tục trên đoạn [a;b].
Khi đó, diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y=f(x),y=g(x) và hai đường thẳng x=a,x=b được tính bởi công thức:
S=a∫b∣f(x)−g(x)∣dx
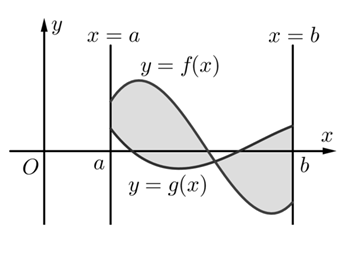
2. Ví dụ minh hoạ: Ứng dụng của tích phân vào bài toán diện tích
Ví dụ 1:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3−x và đồ thị hàm số y=x−x2.
Lời giải:
Phương trình hoành độ giao điểm x3−x=x−x2⇔x3+x2−2x=0⇔⎣⎢⎡x=0x=1x=−2
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=x3−x và đồ thị hàm số y=x−x2 là:
S=−2∫1∣∣x3−x−(x−x2)∣∣dx=1237
Ví dụ 2:
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: y=x3−3x , y=x .
Tính S .
Lời giải:
Phương trình hoành độ giao điểm của hai đồ thị là x3−3x=x ⇔x3−4x=0 ⇒⎣⎢⎡x=−2x=0x=2 .
Vậy S=∣∣∣∣∣∣−2∫0(x3−4x)dx∣∣∣∣∣∣+∣∣∣∣∣∣0∫2(x3−4x)dx∣∣∣∣∣∣ =4+4=8 .
3. Luyện tập củng cố: Ứng dụng của tích phân vào bài toán diện tích
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay