HYPEBOL

• Trên mặt phẳng, nếu hai thiết bị đặt tại các vị trí F1​, F2​ nhận được một tín hiệu âm thanh cùng lúc thì vị trí phát ra tín hiệu cách đều hai điểm F1​,F2​, và do đó, nằm trên đường trung trực của đoạn thẳng F1​F2​. 

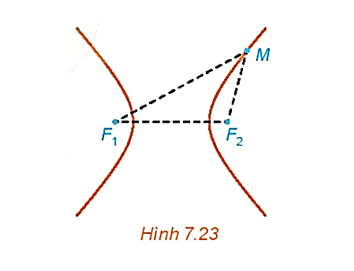
• Cho hai điểm phân biệt cố định F1​, F2​. Đặt F1​F2​=2c. Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho ∣MF1​−MF2​∣=2a  được gọi là đường hypebol. Hai điểm F1​, F2​ được gọi là hai tiêu điểm và F1​F2​=2c được gọi là tiêu cự của hypebol đó.
• Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn thẳng nối hai tiêu điểm đó thì có phương trình a2x2​−b2y2​=1, với a,b>0. 
• Ngược lại, mỗi phương trình có dạng (4)  đều là phương trình của hypebol có hai tiêu điểm F1​(−√a2+b2​;0),  F2​(√a2+b2​;0), tiêu cự 2x=2√a2+b2​  và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng 2a. 
• Phương trình được gọi là phương trình chính tắc của hypebol tương ứng.