Viết phương trình Đường thẳng tổng quát, tham số

1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG

1. Vectơ pháp tuyến của đường thẳng

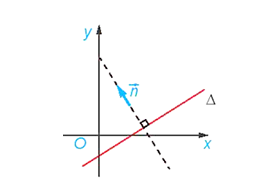
1.1. Định nghĩa: Vectơ n=0 gọi là vectơ pháp tuyến (VTPT) của Δ nếu giá của nó vuông góc với Δ.  

1.2. Nhận xét:

1. Nếu n là một vtpt của đường thẳng d thì k.n,(k=0) cũng là một vtpt của d. 
2. Nếu n là một VTPT của đường thẳng d và u  là một VTCP của đường thẳng d thì n.u=0 
3. Một đường thẳng xác định khi biết một VTPT và mộ điểm nó đi qua.

2. Phương trình tổng quát (PTTQ) của đường thẳng

• Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát dạng ax+by+c=0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax+by+c=0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận n⃗(a;b) là một vectơ pháp tuyến.

1. Đường thẳng d đi qua điểm M(x0​;y0​) và có VTPT n⃗=(A;B) thì có phương trình tổng quát là A(x−x0​)+B(y−y0​)=0. 
2. Ngược lại, trong mặt phẳng với hệ tọa độ Oxy  mọi phương trình dạng: Ax+By+C=0(A2+B2=0) đều là phương trình tổng quát của đường thẳng d  có VTPT n⃗=(A;B).  
3. Một số trường hợp đặc biệt của PTTQAx+By+C=0(A2+B2=0). 

• Nếu A=0 phương trình trở thành By+C=0⇔y=−BC​  đường thẳng song song với trục hoành Ox  và cắt trục tung Oy  tại điểm M(0;−BC​). 
• Nếu B=0 phương trình trở thành Ax+C=0⇔x=−AC​  đường thẳng song song với trục tung Oy và cắt trục hoành Ox  tại M(−AC​;0). 
• Nếu C=0 phương trình trở thành Ax+By=0 đường thẳng đi qua gốc tọa độ O(0;0). 
• Đường thẳng có dạng y=ax+b, (trong đó a được gọi là hệ số góc của đường thẳng ) có VTPT là n⃗=(a;−1) . Ngược lại đường thẳng có VTPT n⃗=(A;B)  thì có hệ số góc là −BA​ 
• Đường thẳng d  đi qua điểm A(a;0) và B(0;b) có phương trình là ax​+by​=1. 

2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

1. Véc tơ chỉ phương của đường thẳng

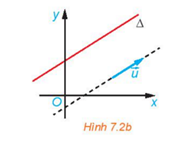
a. Định nghĩa Vectơ u=0 được gọi là vectơ chỉ phương (VTCP) của đường thẳng Δ nếu giá của nó song song hoặc trùng với Δ. 

b. Nhận xét:

• Nếu u là một vtcp của đường thẳng d  thì k.u,(k=0)  cũng là một véc tơ chỉ phương của d 
• Một đường thẳng xác định khi biết một vtcp và một điểm mà nó đi qua.

2. Phương trình tham số của đường thẳng

• Cho đường thẳng Δ  đi qua điểm A(x0​;y0​) và có vectơ chỉ phương u(a;b) . Khi đó điểm M(x;y) thuộc đường thẳng Δ  khi và chỉ khi tồn tại số thực t  sao cho AM=tu , hay {​x=x0​+aty=y0​+bt​   (2)
• Hệ (2) được gọi là phương trình tham số của đường thẳngΔ  (t là tham số).

1. Đường thẳng d đi qua điểm M(x0​;y0​) và có vtcp u=(a;b)  thì có phương trình tham số là {​x=x0​+aty=y0​+bt​. ( Mỗi điểm M bất kỳ thuộc đường thẳng (d) tương ứng với duy nhất một số thực t∈R và ngược lại).

Nhận xét‎‎‎‎: A∈Δ⇔A(x0​+at;y0​+bt),t∈R 

Trong mặt phẳng với hệ tọa độ Oxy, mọi phương trình dạng {​x=x0​+aty=y0​+bt​   với a2+b2=0 đều là phương trình của đường thẳng d  có một vtcp là u=(a;b). 

3. Phương trình chính tắc của đường thẳng

• Đường thẳng d đi qua điểm M(x0​;y0​) và có vtcp u=(a;b) với a=0,b=0 có phương trình chính tắc là: ax−x0​​=by−y0​​ 

3. LIÊN HỆ GIỮA VTCP VÀ VTPT

1. Từ nhận xét “Nếu n là một VTPT của đường thẳng d và u là một VTCP của đường thẳng d thì n.u=0 ” ta rút ra được: nếu n=(A;B) là một VTPT của đường thẳng d  thì một VTCP của d  là u=(B;−A) (hoặc u=(−B;A) )
2. Từ nhận xét “Nếu n  là một VTPT của đường thẳng d  và u  là một VTCP của đường thẳng d  thì n.u=0 ” ta rút ra được: nếu u=(a;b)  là một VTCP của đường thẳng d thì một VTPT của d là n=(−b;a)  (hoặc n=(b;−a) ).

• Hai nhận xét trên giúp ích rất nhiều trong việc chuyển đổi qua lại giữa các dạng phương trình đường thẳng. Từ PTTQ ta có thể chuyển sang PTTS và ngược lại.