1. Bài giảng: Hình lăng trụ và hình hộp
HÌNH LĂNG TRỤ ĐỨNG và HÌNH HỘP
1. Hình lăng trụ đứng
- Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với hai mặt đáy.
- Các mặt bên là các hình chữ nhật.
- Các mặt bên vuông góc với hai đáy.
2. Hình lăng trụ đều
- Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
3. Hình hộp đứng
- Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
4. Hình hộp chữ nhật
- Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
- Tất cả các mặt đều là hình chữ nhật.
- Đường chéo d=√a2+b2+c2 với a,b,c là 3 kích thước.
5. Hình lập phương
- Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
| Tên | Hình vẽ | Tính chất cơ bản |
| Hình lăng trụ đứng | 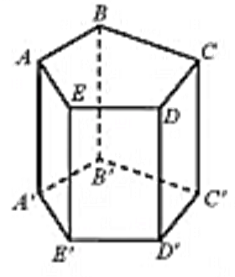 |
- Cạnh bên vuông góc với hai đáy - Mặt bên là các hình chữ nhật. |
| Hình lăng trụ đều | 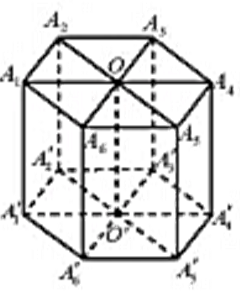 |
- Hai đáy là hai đa giác đều. - Mặt bên là các hình chữ nhật. - Cạnh bên và đường nối tâm hai đáy vuông góc vơi hai đáy |
| Hình hộp đứng | 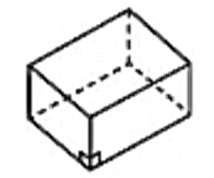 |
- Bốn mặt bên là hình chữ nhật. - Hai đáy là hình bình hành |
| Hình hộp chữ nhật | 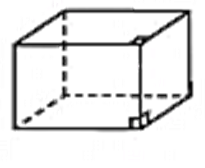 |
- Sáu mặt là hình chữ nhật. - Độ dài a,b,c của ba cạnh cùng đi qua một ssinhr gọi là ba kích thước của hình hộp chữ nhật. - Độ dài đường chéo d được tính theo a kích thước: d=√a2+b2+c2. |
| Hình lập phương | 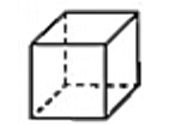 |
- Sáu mặt là hình vuông. - Độ dài đường chéo d được tính theo độ dài cạnh a: d=a√3. |
2. Ví dụ minh hoạ: Hình lăng trụ và hình hộp
Ví dụ 1:
Cho hình bình hành ABCD .
Vẽ các tia Ax,By,Cz,Dt song song, cùng hướng nhau và không nằm trong mp(ABCD) .
Mp (α) cắt Ax,By,Cz,Dt lần lượt tạiA′,B′,C′,D′ .
Khẳng định nào sau đây sai?
Lời giải:


AB//DCAA′//DD′AB,AA′⊂(ABB′A′)DC,DD′⊂(DD′C′C)⎭⎪⎪⎪⎬⎪⎪⎪⎫⇒(ABB′A′)//(DD′C′C) . Câu B đúng.
Mặt khác
(α)∩(ABB′A′)=A′B′(α)∩(DCC′D′)=C′D′(ABB′A′)//(DCC′D′)⎭⎪⎬⎪⎫⇒A′B′//C′D′
(α)∩(ADD′A′)=A′D′(α)∩(BCC′B′)=C′B′(ABB′A′)//(DCC′D′)⎭⎪⎬⎪⎫⇒A′D′//C′B′
Do đó câu A đúng.
O,O′ lần lượt là trung điểm của AC,A′C′ nên OO′ là đường trung bình trong hình thang AA′C′C . Do đó OO′// AA′ . Câu D đúng.
Ví dụ 2:
Cho hình lăng trụ ABC.A′B′C′. Gọi M,N lần lượt là trung điểm của BB′ và CC′ .
Gọi Δ là giao tuyến của hai mặt phẳng (AMN) và (A′B′C′) .
Khẳng định nào sau đây đúng?
Lời giải:


Ta có ⎩⎪⎨⎪⎧MN⊂(AMN)B′C′⊂(A′B′C′)MN∥B′C′ ⇒ Δ là giao tuyến của hai mặt phẳng (AMN) và (A′B′C′) sẽ song song với MN và B′C′ . Suy ra Δ∥BC .
3. Luyện tập củng cố: Hình lăng trụ và hình hộp
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay