Hai mặt phẳng song song

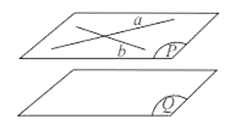
1. Vị trí tương đối giữ 2 mặt phẳng (α) và (β) có 3 vị trí tương đối

Trường hợp 1: (P) và (Q) có ba điểm chung không thẳng hàng, ta nói hai mặt phẳng (P) và (Q) trùng nhau, kí hiệu (P)≡(Q). 

Trường hợp 2: (P) và (Q) phân biệt và có một điềm chung, ta nói (P) và (Q) cắt nhau theo giao tuyến d  đi qua điểm chung, ki hiệu (P)∩(Q)=d. 

Trường hợp 3: (P) và (Q) không có bất kì điểm chung nào, nghĩa là (P)∩(Q)=∅ , ta nói (P)  và (Q)  song song với nhau, kí hiệu (P)//(Q)  hoặc (Q)//(P). 

(P)≡(Q)                                     (P)  cắt (Q)                                    (P)//(Q) 

 Định nghĩa: Hai mặt phẳng (α) và (β)  được gọi là song song với nhau nếu chúng không có điểm chung; (α)//(β)⇔(α)∩(β)=∅  

Chú ý: (α)//(β),d⊂(α)⇒d//(β)  

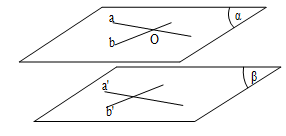
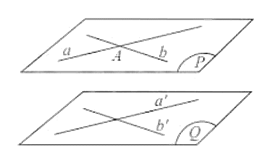
2. Điều kiện để hai mặt phẳng song song

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a,b và a,b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

Hệ quả: Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a,b và a,b lần lượt song song với hai đường thẳng a’,b’ nằm trong mặt phẳng (β)  thì mặt phẳng (α)  song song với mặt phẳng (β). 

⎩⎪⎪⎪⎨⎪⎪⎪⎧​​a,b⊂(α)a∩b=Oa//a′,b//b′a′,b′⊂(β)​⇒(α)//(β)

Lưu ý: Nếu hai mặt phẳng song song với nhau thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.

3. Tính chất của hai mặt phẳng song song

Định lý 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chi một mặt phằng song song với mặt phẳng đó.

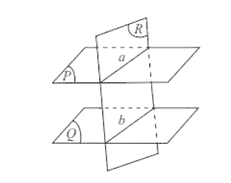
Định lý 3: Cho hai mặt phẳng (P)  và (Q)  song song với nhau. Nếu (R)  cắt (P)  thì cắt (Q)  và hai giao tuyến của chúng song song với nhau.

4. Định lý talet trong không gian

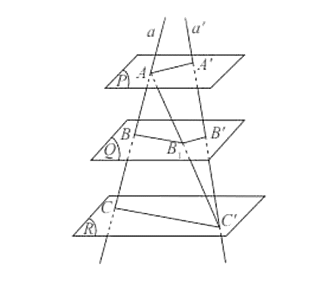
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ A′B′AB​=B′C′BC​=C′A′CA​ 

5. Hình lăng trụ và hình hộp

Hình lăng trụ: Cho hai mặt phẳng (P)  và (P′)  song song với nhau. Trên (P)  cho đa giác lồi A1​A2​…An​ . Qua các đỉnh của đa giác này, ta vẽ các đường thẳng song song với nhau và cắt (P′)  lần lượt tại A1 ′ ​,A2 ′ ​,…,An ′ ​ . Hình tạo bởi các hình bình hành A1​A2​A2 ′ ​A1 ′ ​,A2​A3​A3 ′ ​A2 ′ ​,…,An​A1​A1 ′ ​An ′ ​  và hai đa giác A1​A2​…An​,A1 ′ ​A2 ′ ​…An ′ ​  gọi là hình lăng trụ, kí hiệu A1​A2​…An​⋅A1 ′ ​A2 ′ ​…An ′ ​. 

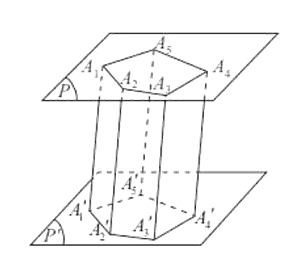
Trong hình lăng trụ A1​A2​…An​⋅A1 ′ ​A2 ′ ​…An ′ ​ , ta gọi:

Hai đa giác A1​A2​…An​  và A1 ′ ​A2 ′ ​…An ′ ​  là hai mặt đáy nằm trên hai mặt phẳng song song;

Các điểm A1​,A2​,…,An​,A1 ′ ​,A2 ′ ​,…,An ′ ​  là các đĩnh;

Các hình bình hành A1​A2​A2 ′ ​A1 ′ ​,A2​A3​A3 ′ ​A2 ′ ​,…,An​A1​A1 ′ ​An ′ ​  là các mặt bên;

Các đoạn thẳng A1​A1 ′ ​,A2​A2 ′ ​,…,An​An ′ ​  là các cạnh bên.

Các cạnh bên song song vả bằng nhau.

Các cạnh của hai đa giác đáy là các cạnh đáy. Các cạnh đáy tương ứng song song và bằng nhau.

Chú ý: Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác, ... tương ứng được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác, ...

Hình hộp: là hình lăng trụ có đáy là hình bình hành.

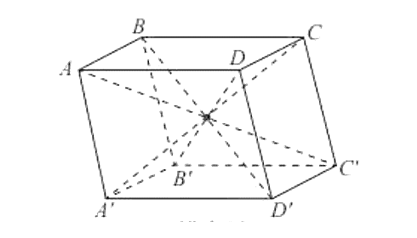
Trong một hình hộp ta có:

Sáu mặt là sáu hình bình hành. Mỗi mặt đều có một mặt song song với nó. Hai mặt như thế gọi là hai mặt đối diện; - Hai đỉnh không cùng nằm trên một mặt gọi là hai đỉnh đối diện;

Đoạn thẳng nối hai đình đối diện gọi là đường chéo;

Bốn đường chéo cắt nhau tại trung điểm của mỗi đường.