1. Ví dụ minh hoạ: Thể tích
Ví dụ 1:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với mặt đáy một góc 600 .
Tính theo a thể tích V của khối chóp S.ABCD .
Lời giải:

Gọi O=AC∩BD. Do S.ABCD là hình chóp đều nên SO⊥(ABCD) .
Suy ra OB là hình chiếu của SB trên (ABCD) .
Khi đó 600=SB,(ABCD)=SB,OB=SBO .
Tam giác vuông SOB , có SO=OB.tanSBO=2a√6.
Diện tích hình vuông ABC là SABCD=AB2=a2.
Vậy VS.ABCD=31SABCD.SO=6a3√6.
Ví dụ 2:
Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa mặt bên với mặt đáy bằng 600 .
Tính theo a thể tích V của khối chóp S.ABC .
Lời giải:
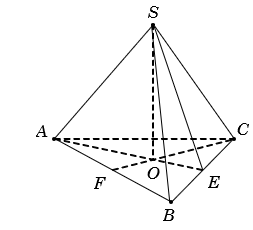
Gọi E, F lần lượt là trung điểm BC, BA vàO=AE∩CF .
Do S.ABC là hình chóp đều nên SO⊥(ABC) .
Khi đó 600=(SBC),(ABC)=SE,OE=SEO .
Tam giác vuông SOE , có
SO=OE.tanSEO=3AE.tan600=6a√3.√3=2a .
Diện tích tam giác đều ABC là SΔABC=4a2√3 .
Vậy VS.ABC=31SΔABC.SO=24a3√3.
2. Luyện tập củng cố: Thể tích
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay