1. Bài giảng: Đường thẳng vuông góc với mặt phẳng
Đường thẳng vuông góc với mặt phẳng
1. Định nghĩa
- Đường thẳng d được gọi là vuông góc với mặt phẳng (α) nếu d vuông góc với mọi đường thằng a thuộc mặt phẳng (α).
- Kí hiệu: d⊥(α) hay (α)⊥d.
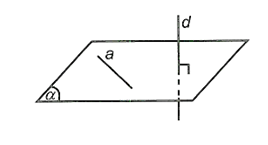
d⊥(α)⇔d⊥a,∀a⊂(α)
- Đường thẳng vuông góc với mặt phẳng khi và chỉ khi nó vuông góc với hai đường thẳng cắt nhau cùng thuộc mặt phẳng ấy.
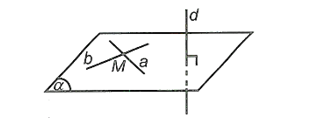
⎩⎪⎪⎪⎨⎪⎪⎪⎧d⊥ad⊥ba⊂(α),b⊂(α)a∩b=M⇒a⊥(α).
- Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
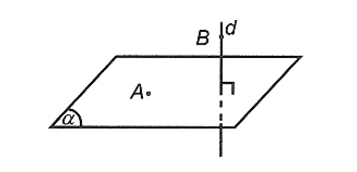
- Có duy nhất đường thẳng d đi qua B và vuông góc với (α).
- Có duy nhất mặt phẳng (α) đi qua A và vuông góc với d.
2. Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng
a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì vuông góc với đường thẳng kia
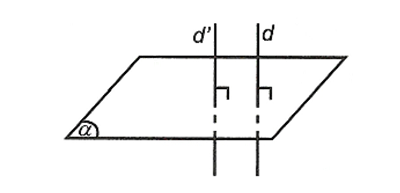
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
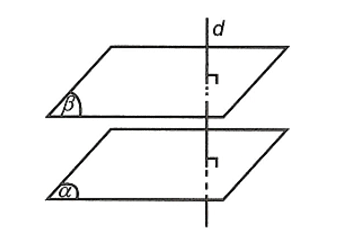
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì vuông góc với mặt phẳng kia
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
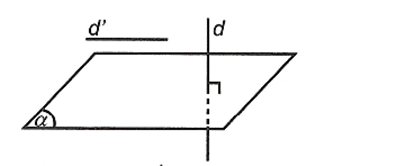
a) Cho đường thẳng a song song với mặt phẳng (α). Đường thẳng nào vuông góc với (α) thì cũng vuông góc với a.
b) Nếu đường thẳng a và mặt phẳng (α) (không chứa a ) cùng vuông góc với một đường thẳng b thì chúng song song với nhau.
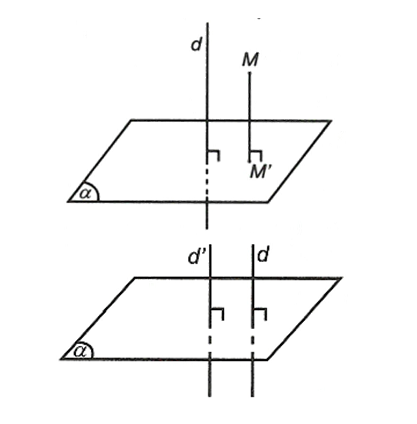
3. Phép chiếu vuông góc
Cho đường thẳng d⊥(α) . Phép chiếu song song theo phương d lên mặt phẳng (α) được gọi là phép chiếu vuông góc lên mặt phẳng (α)
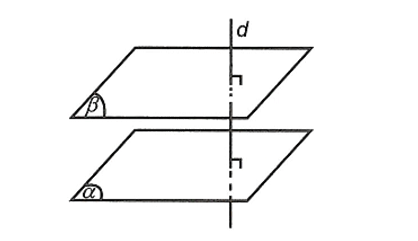
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì vuông góc với mặt phẳng kia
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
a) Cho đường thẳng a song song với mặt phẳng (α). Đường thẳng nào vuông góc với (α) thì cũng vuông góc với a.
b) Nếu đường thẳng a và mặt phẳng (α) (không chứa a ) cùng vuông góc với một đường thẳng b thì chúng song song với nhau.
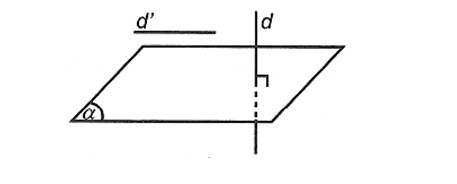
4. Phép chiếu vuông góc
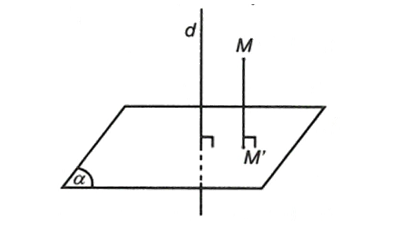
Cho đường thẳng d⊥(α). Phép chiếu song song theo phương d lên mặt phẳng (α) được gọi là phép chiếu vuông góc lên mặt phẳng (α)
2. Ví dụ minh hoạ: Đường thẳng vuông góc với mặt phẳng
Ví dụ 1:
Cho tứ diện ABCD Gọi H là trực tâm của tam giác BCD và AH vuông góc với mặt phẳng đáy.
Khẳng định nào dưới đây là đúng?
Lời giải:

 Vì AH vuông góc với mp(BCD) suy ra AH⊥CD. (1)
Vì AH vuông góc với mp(BCD) suy ra AH⊥CD. (1)
Mà H là trực tâm của tam giác BCD ⇒BH⊥CD. (2)
Từ (1),(2) suy ra {CD⊥AHCD⊥BH⇒CD⊥(ABH)⇒CD⊥AB.
Ví dụ 2:
Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B và SA vuông góc với mặt phẳng (ABC) .
Gọi M ,N lần lượt là hình chiếu vuông góc của A trên cạnh SB và SC .
Khẳng định nào sau đây sai?
Lời giải:

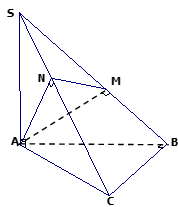
Ta có: SA⊥(ABC)⇒SA⊥BC mà BC⊥AB ⇒BC⊥(SAB) , AM⊂(SAB) ⇒BC⊥AM .
Vậy {AM⊥SBAM⊥BC⇒AM⊥(SBC) ⇒AM⊥SC ⇒ Đáp án AM⊥SC đúng.
Vì {AM⊥(SBC)MN⊂(SBC)⇒AM⊥MN ⇒ Đáp án AM⊥MN đúng.
SA⊥(ABC)⇒SA⊥BC ⇒ Đáp án SA⊥BC đúng.
Vậy AN⊥SB sai.
3. Luyện tập củng cố: Đường thẳng vuông góc với mặt phẳng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay