1. Bài giảng: Tập Hợp
Tập hợp
1. Tập hợp
2. Tập con và hai tập hợp bằng nhau
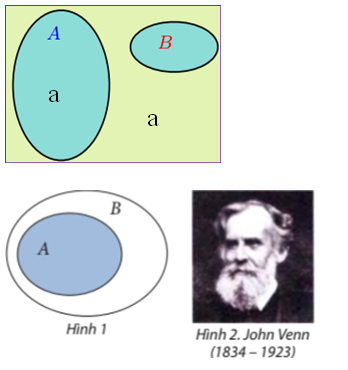
- Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A⊂B (đọc là A chứa trong B), hoặc B⊃A (đọc là B chứa A)
- A⊂A và ∅⊂A với mọi tập hợp A.
- Nếu A không phải là tập con của B thì ta kí hiệu A⊂B (đọc là A không chứa trong B hoặc B không chứa A ).
- Nếu A⊂B hoặc B⊂A thì ta nói A và B có quan hệ bao hàm.
3. Hai tập hợp bằng nhau
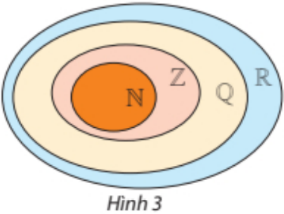
4. Các tập hợp số đã học
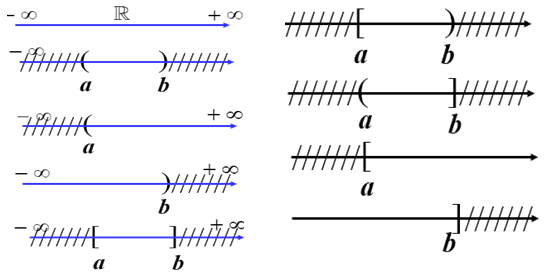
5. Các tập con thường dùng của R:
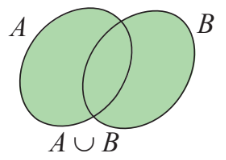
6. Hợp của hai tập hợp
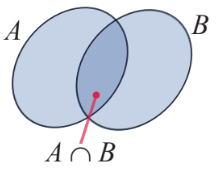
7. Giao của hai tập hợp
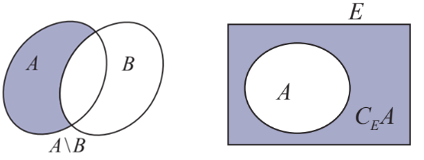
8. Hiệu và phần bù của hai tập hợp
2. Ví dụ minh hoạ: Tập Hợp
Ví dụ 1:
Lớp 10C có 7 Hs giỏi Toán, 5 Hs giỏi Lý, 6 Hs giỏi Hoá, 3 Hs giỏi cả Toán và Lý, 4 Hs giỏi cả Toán và Hoá, 2 Hs giỏi cả Lý và Hoá, 1 Hs giỏi cả 3 môn Toán, Lý, Hoá.
Hỏi số HS giỏi ít nhất một môn ( Toán, Lý, Hoá ) của lớp 10C là?
Lời giải:
g/s: A= “Hs giỏi toán”; B= “Hs giỏi lý”; C= “Hs giỏi hóa”
A∪B∪C= “Hs giỏi toán, hóa, lý”:7+5+6=18 .
(A∩B)∪(A∩C)∪(B∩C)= “ số Hs giỏi hai môn”:3+4+2=9 .
Số Hs giỏi ít nhất một môn: toán, lý, hóa là:
A∪B∪C\((A∩B)∪(A∩C)∪(B∩C))=18−9=9 .
Câu B, C, D do Hs không hiểu các phép toán tập hợp.
Ví dụ 2:
Có 45 học sinh giỏi, mỗi em giỏi ít nhất một môn.
Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh.
Có 8 em giỏi đúng hai môn Văn, Toán; Có 7 em giỏi đúng hai môn Toán, Anh; Có 6 em giỏi đúng hai môn Anh, Văn.
Hỏi: Có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?
Lời giải:
Theo giả thiết ta có:n(V)=22, n(T)=25 , n(A)=20,
n(V∩T)= 8, n(T∩A)=7, n(V∩A)=6,n(A∪B∪C)=45 .
n(V∪A∪T)=n(V)+n(A)+n(T)−n(V∩A)−n(A∩T)−n(T∩V)+n(V∩A∩T)
⇒45=22+20+25−6−7−8+n(V∩A∩T)
⇒n(V∩A∩T)=19
3. Luyện tập củng cố: Tập Hợp
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay