1. Bài giảng: Tiệm cận của đồ thị hàm số
Tiệm cận của đồ thị hàm số
1. Đường tiệm cận ngang
Định nghĩa: Đường thẳng y=m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số f(x) nếu:
x→−∞limf(x)=m hoặc x→+∞limf(x)=m
Đường thẳng y=m là tiệm cận ngang của đồ thị hàm số y=f(x) được minh hoạ như hình vẽ dưới đây
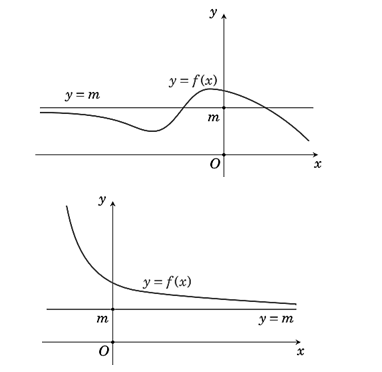
a) x→−∞limf(x)=m
b) x→+∞limf(x)=m
Các bước tìm đường tiệm cận ngang:
Bước 1: Tính giới hạn x→−∞limf(x) và x→+∞limf(x)
Bước 2: Xem ở “vị trí ” nào ra kết quả hữu hạn thì ta kết luận có tiệm cận ngang ở “vị trí” đó
2. đường tiệm cận Đứng (TCĐ)
Định nghĩa: Đường thẳng x=a gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y=f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
x→a−limf(x)=+∞ , x→a+limf(x)=+∞ , x→a−limf(x)=−∞ , x→a+limf(x)=−∞
Đường thẳng x=a là tiệm cận đứng của đồ thị hàm số y=f(x) được minh hoạ như hình vẽ dưới đây
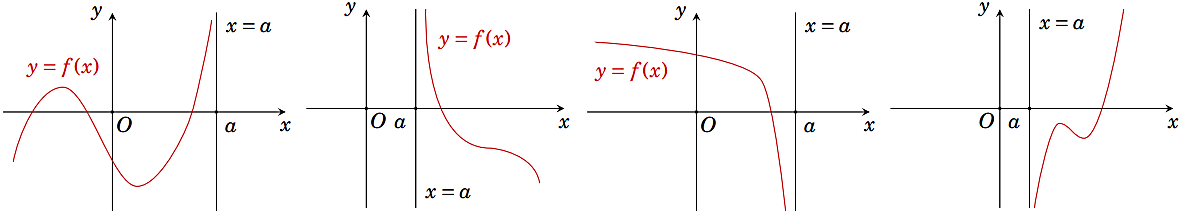
a) x→a−limf(x)=+∞ b) x→a+limf(x)=+∞ c) x→a−limf(x)=−∞ d) x→a+limf(x)=−∞
Các bước tìm đường tiệm cận đứng:
Bước 1: Tìm nghiệm của mẫu, giả sử nghiệm đó là x=x0
Bước 2: Tính giới hạn một bên tại x=x0.
Nếu xảy ra x→x0−limf(x)=∞ hoặc x→x0+limf(x)=∞ thì ta kết luận x=x0 là đường tiệm cận đứng.
3. Đường tiệm cận xiên (TCX)
Định nghĩa: Đường thẳng y=ax+b(a=0) gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y=f(x) nếu:
x→−∞lim[f(x)−(ax+b)]=0 hoặc x→+∞lim[f(x)−(ax+b)]=0
Đường thẳng y=ax+b là tiệm cận xiên của đồ thị hàm số y=f(x) được minh hoạ như hình bên dưới:
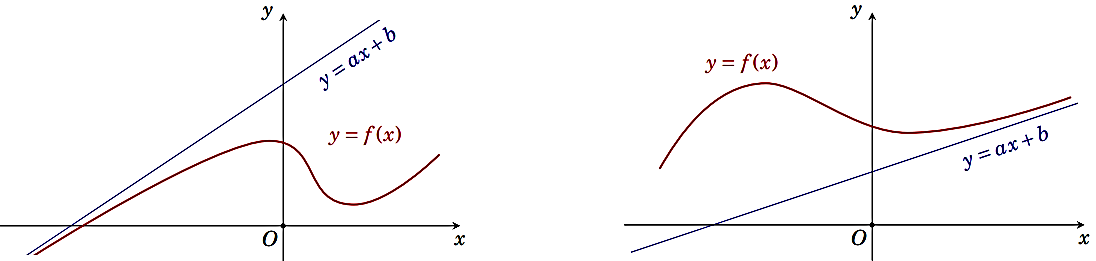
a) x→−∞lim[f(x)−(ax+b)]=0 b) x→+∞lim[f(x)−(ax+b)]=0
Các bước tìm đường tiệm cận xiên: ta xác định hệ số của a và b trong các trường hợp sau
Bước 1: Tính a=x→+∞limxf(x) , b=x→+∞lim[f(x)−ax]
Bước 2: Tính a=x→−∞limxf(x) , b=x→−∞lim[f(x)−ax]
2. Ví dụ minh hoạ: Tiệm cận của đồ thị hàm số
Ví dụ 1:
Cho hàm số y=f(x) có đồ thị như hình vẽ.

Đồ thị hàm số có đường tiệm cận đứng bằng
Lời giải:
Dựa vào đồ thị ta thấy đồ thị hàm số có đường tiệm cận đứng x=−1 .
Ví dụ 2:
Cho hàm số y=f(x) có đồ thị như hình vẽ.

Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận đứng?
Lời giải:
Từ đồ thị ta thấy
x→−2+limf(x)=+∞ và x→−2−limf(x)=−∞ nên đường thẳng x=−2 là một đường tiệm cận đứng.
x→2−limf(x)=+∞ và x→2+limf(x)=−∞ nên đường thẳng x=2 là một đường tiệm cận đứng.
3. Luyện tập củng cố: Tiệm cận của đồ thị hàm số
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay