Tính đơn điệu của hàm số

1. Định nghĩa: 

Định nghĩa: Cho hàm số y=f(x) xác định trên K với K là một khoảng, một đoạn hoặc một nửa khoảng

Hình 1. Hàm số đồng biến trên (a;b) 

• Hàm số y=f(x) được gọi là đồng biến trên K  nếu ∀x1​, x2​∈K, x1​<x2​⇒f(x1​)<f(x2​).  Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải (Hình 1)

               

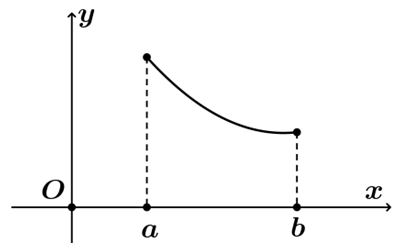
Hình 2. Hàm số nghịch biến trên (a;b) 

• Hàm số y=f(x) được gọi là nghịch biến trên K nếu ∀x1​, x2​∈K, x1​<x2​⇒f(x1​)>f(x2​) 
• Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (Hình 2)
• Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K. 
• Khi xét tính đơn điệu mà không chỉ rõ tập K thì ta hiểu là xét trên tập xác định của hàm số đó.

2. Liên hệ giữa đạo hàm và tính đơn điệu:

Định lí 1: Cho hàm số y=f(x) có đạo hàm trên khoảng K. 

• Nếu f′(x)≥0, ∀x∈K  và f′(x)=0 xảy ra tại một số hữu hạn điểm trên K thì hàm số y=f(x) đồng biến trên khoảng K.  
• Nếu f′(x)≤0, ∀x∈K  và f′(x)=0 xảy ra tại một số hữu hạn điểm trên K thì hàm số y=f(x) nghịch biến trên khoảng K.  

Chú ý: Nếu hàm số y=f(x) đồng biến trên tập K hoặc nghịch biến trên tập K thì hàm số y=f(x) còn được gọi là đơn điệu trên tập K⊂R. 

Định lí 2: Cho hàm số y=f(x) có đạo hàm trên tập K⊂R, trong đó K là một khoảng, đoạn hoặc nửa khoảng. Nếu f′(x)≥0 (hoặc f′(x)≤0) với mọi x thuộc K  và f′(x)=0 chỉ tại một số hữu hạn điểm của K thì hàm số y=f(x) đồng biến (hoặc nghịch biến) trên K.