Cực trị hàm số

1. Cực trị của hàm số

Định nghĩa: Cho hàm số y=f(x) liên tục trên khoảng (a;b) và điểm x0​∈(a;b). 

• Nếu tồn tại số h>0 sao cho f(x)<f(x0​) với mọi x∈(x0​−h;x0​+h)⊂(a;b) và x=x0​  thì ta nói hàm số f(x)  đạt cực đại tại x0​. 
• Nếu tồn tại số h>0 sao cho f(x)>f(x0​) với mọi x∈(x0​−h;x0​+h)⊂(a;b) và x=x0​ thì ta nói hàm số f(x)  đạt cực tiểu tại x0​. 

Ghi chú:

• Nếu hàm số y=f(x) đạt cực đại tại x0​ thì x0​ được gọi là điểm cực đại của hàm số, f(x0​) được gọi là giá trị cực đại của hàm số, kí hiệu fC​ hay yC​, còn điểm M(x0​;f(x0​)) được gọi là điểm cực đại của đồ thị hàm số.
• Nếu hàm số y=f(x) đạt cực tiểu tại x0​  thì x0​ được gọi là điểm cực tiểu của hàm số, f(x0​)  được gọi là giá trị cực tiểu của hàm số, kí hiệu fCT​ hay yCT​ , còn điểm M(x0​;f(x0​))  được gọi là điểm cực tiểu của đồ thị hàm số.
• Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (còn gọi là cực đại) và giá trị cực tiểu (còn gọi là cực tiểu) được gọi chung là giá trị cực trị (hay cực trị) của hàm số.
• Nếu hàm số y=f(x) có đạo hàm trên khoảng (a;b) và có điểm cực trị là x0​∈(a;b) thì f′(x0​)=0 

Định lí: Giả sử hàm số y=f(x) liên tục trên khoảng K=(x0​−h;x0​+h) và có đạo hàm trên K  hoặc trên K\{x0​}, với h>0. 

• Nếu f′(x)>0  trên khoảng (x0​−h;x0​)  và f′(x0​)<0  trên khoảng (x0​;x0​+h)  thì x0​  là một điểm cực đại của hàm số f(x). 
• Nếu f′(x)<0  trên khoảng (x0​−h;x0​)  và f′(x0​)>0  trên khoảng (x0​;x0​+h)  thì x0​  là một điểm cực tiểu của hàm số f(x). 

Nhận xét: Định lí trên có thể hiểu một cách đơn giản như sau: Điều kiện đủ để hàm số y=f(x) đạt cực trị tại một điểm x0​ là đạo hàm f′(x) đổi dấu khi x  qua x0​  với x∈(x0​−h;x0​+h). 

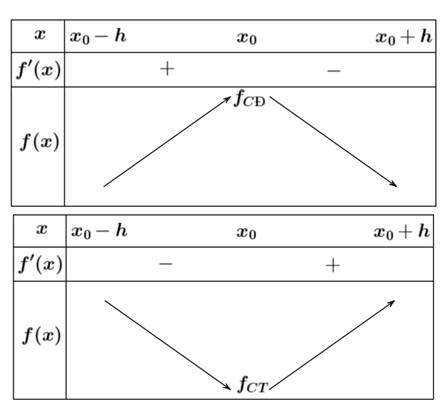
Nếu hàm số y=f(x) đạt cực tr.ị tại x0​ thì f′(x0​)=0 hoặc f′(x0​) không tồn tại.

2. Các tên gọi từ đồ thị hàm số: 

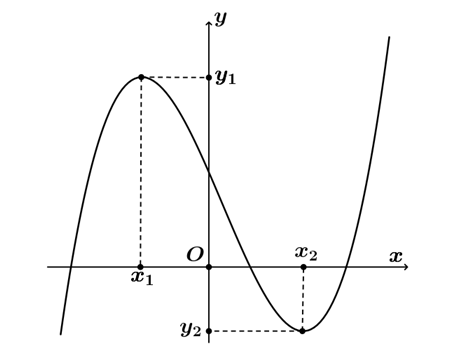
• (x1​;y1​) là điểm cực đại của đồ thị hàm số trong đó: x1​ là điểm cực đại của hàm số; y1​ là giá trị cực đại của hàm số.

• (x2​;y2​) là điểm cực tiểu của đồ thị hàm số trong đó: x2​ là điểm cực tiểu của hàm số; y2​ là giá trị cực tiểu của hàm số.

.