Không gian mẫu - biến cố

I. BIẾN CỐ

1. Phép thử ngẫu nhiên

• Phép thử ngẫu nhiên (gọi tắt là phép thử) là một phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

2. Không gian mẫu

• Tập hợp các kết quả có thể xẩy ra của một phép thử được gọi là không gian mẫu của phép thử đó và ký hiệu là Ω. 

Ví dụ: Khi ta tung một đồng xu có 2 mặt, ta hoàn toàn không biết trước được kết quả của nó, tuy nhiên ta lại biết chắc chắn rằng đồng xu rơi xuống sẽ ở một trong 2 trạng thái: sấp (S) hoặc ngửa (N).Không gian mẫu của phép thử là Ω={S;N} 

3. Biến cố

• Một biến cố A (còn gọi là sự kiện A) liên quan tới phép thử T là biến cố mà việc xẩy ra hay không xẩy ra của nó còn tùy thuộc vào kết quả của T. 
• Mỗi kết quả của phép thử T làm cho biến cố A xảy ra được gọi là một kết quả thuận lợi cho A. 

4. Tập hợp các kết quả thuận lợi

• Tập hợp các kết quả thuận lợi cho A được kí hiệu bởi n(A) hoặc ΩA​. Để đơn giản, ta có thể dùng chính chữ A để kí hiệu tập hợp các kết quả thuận lợi cho A. 
• Khi đó ta cũng nói biến cố A được mô tả bởi tập A. 

5. Biến cố chắc chắn

• Biến cố chắc chắn là biến cố luôn xẩy ra khi thực hiện hiện phép thử T. Biến cố chắc chắn được mô tả bởi tập Ω và được ký hiệu là Ω. 

6. Biến cố không thể

• Biến cố không thể là biến cố không bao giờ xẩy ra khi thực hiện phép thử T.
• Biến cố không thể được mô tả bởi tập ∅. 

7. Các phép toán trên biến cố

Tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A. Giả sử A  và B  là hai biến cố liên quan đến một phép thử. Ta có:

• Tập A∪B được gọi là hợp của các biến cố A  và B. 
• Tập A∩B được gọi là giao của các biến cố A  và B. 
• Nếu A∩B=∅ thì ta nói A  và B  xung khắc.

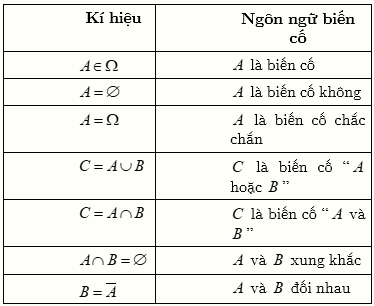
8. Bảng đọc ngôn ngữ biến cố.

II. ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT

1. Định nghĩa cổ điển của xác suất:

• Cho T là một phép thử ngẫu nhiên với không gian mẫu Ω là một tập hữu hạn. Giả sử A là một biến cố được mô ta bằng ΩA​⊂Ω.  Xác suất của biến cố A, kí hiệu bởi P(A), được cho bởi công thức:

Chú ý:  0≤P(A)≤1.

                       P(Ω)=1, P(∅)=0. 

2. Định nghĩa thống kê của xác suất

• Xét phép thử ngẫu nhiên T và một biến cố A liên quan tới phép thử đó. Nếu tiến hành lặp đi lặp lại N lần phép thử T và thống kê số lần xuất hiện của A là n. 
• Khi đó xác suất của biến cố A được định nghĩa như sau: P(A)=Nn​.