1. Bài giảng: Hàm số bậc hai, đồ thị hàm số bậc 2 và ứng dụng
HÀM SỐ BẬC HAI, ĐỒ THỊ HÀM SỐ BẬC 2 VÀ ỨNG DỤNG
1. ĐỊNH NGHĨA
- Hàm số bậc hai là hàm số cho bởi công thức: y=ax2+bx+c,
- trong đó x là biến số, a,b,c là các hằng số và a=0.
- Tập xác định của hàm số bậc hai là R.
- Khi a=0,b=0, hàm số trở thành hàm số bậc nhất y=bx+c.
- Khi a=b=0, hàm số trở thành hàm hằng y=c.
2. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI
a) Đồ thị hàm số y=ax2,a=0 là một parabol có đỉnh là gốc tọa độ, có trục đối xứng là trục tung (là đường thẳng x=0). Parabol này quay bề lõm lên trên nếu a>0, xuống dưới nếu a<0.
b) Đồ thị hàm số y=ax2+bx+c,a=0 là một parabol có:
- Đỉnh I(−2ab;−4aΔ).
- Trục đối xứng là đường thẳng x=−2ab.
- Bề lõm hướng lên trên nếu a>0, hướng xuống dưới nếu a<0.
- Giao điểm với trục tung là M(0;c).
- Số giao điểm với trục hoành bằng số nghiệm của phương trình ax2+bx+c=0.
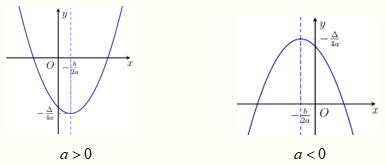
3. BẢNG BIẾN THIÊN
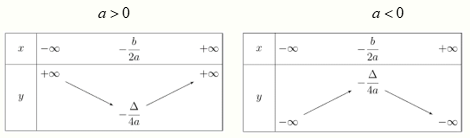
- Khi a>0, hàm số đồng biến trên khoảng (−2ab;+∞) và nghịch biến trên khoảng (−∞;−2ab)
- Khi a<0, hàm số đồng biến trên khoảng (−∞;−2ab) và nghịch biến trên khoảng (−2ab;+∞).
Để vẽ đường parabol y=ax2+bx+c ta tiến hành theo các bước sau:
Bước 1. Xác định toạ độ đỉnh I(−2ab;−4aΔ);
Bước 2. Vẽ trục đối xứng x=−2ab;
Bước 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol.
Bước 4. Vẽ parabol.
2. Ví dụ minh hoạ: Hàm số bậc hai, đồ thị hàm số bậc 2 và ứng dụng
Ví dụ 1:
Hàm số y=2x2−3x+1 có đồ thị hàm số ở dưới. Chọn phương án chính xác:

Lời giải:
Hàm số đồng biến trên khoảng (43;+∞) và nghịch biến trên khoảng (−∞;43)
Ví dụ 2:
Cho đồ thị hàm số như dưới:
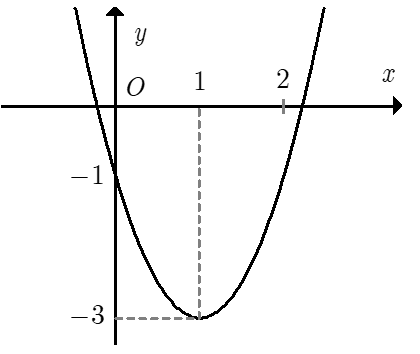
Khẳng định nào sau đây là sai?
Lời giải:
Hàm số trên nghịch biến trên khoảng (−∞;1) và đồng biến trên khoảng (1;+∞)
3. Luyện tập củng cố: Hàm số bậc hai, đồ thị hàm số bậc 2 và ứng dụng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay