1. Bài giảng: Đường thẳng song song đường thẳng
Đường thẳng song song đường thẳng
1. Vị trí tương đối của hai đường thẳng trong không gian
a và b đồng phẳng
- a cắt b⇔a∩b=M.
- a//b⇔a∩b=∅.
- a≡b⇔a∩b=a.
không có mp nào chứa a và b, ta nói a và b chéo nhau.
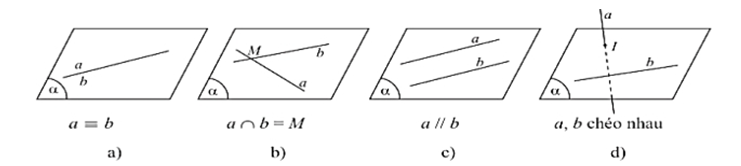
- Hai đường thẳng được gọi là song song nếu chúng cùng nằm trên một mặt phẳng và không có điểm chung
- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
- Cho hai đường thẳng song song a và b. Có duy nhất một mặt phẳng chứa hai đường thẳng đó, kí hiệu mp(a,b).
2. Các tính chất cơ bản về hai đường thẳng song song.
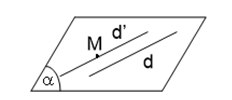
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Ký hiệu: M∉d⇔∃!d′:M∈d′,d′//d
Nhận xét: Hai đt song song a và b xác định một mp, kh(a,b)
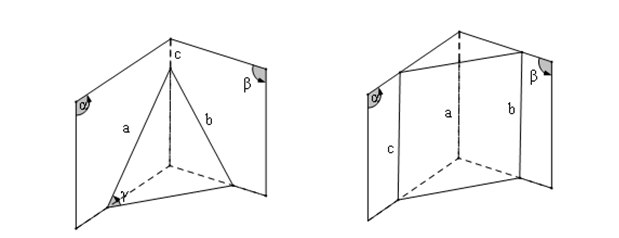
Nếu ba mp phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc dồng qui hoặc đôi một song song với nhau.
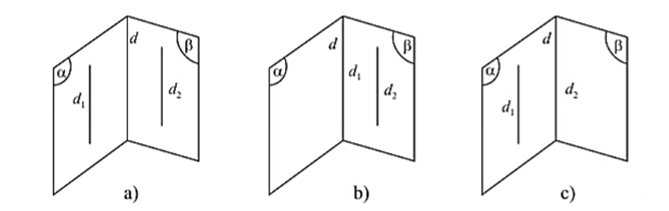
Nếu hai mp phân biệt lần lượt chứa hai đt song song thì giao tuyến của chúng (nếu có) cũng song song với hai đt đó hoặc trùng với một trong hai đt đó.
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.⎩⎪⎨⎪⎧a=ba//c⇔a//bb//c
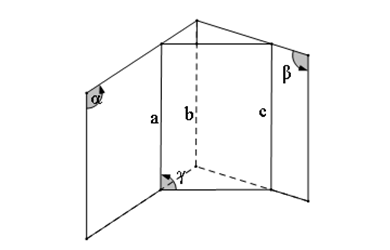
2. Ví dụ minh hoạ: Đường thẳng song song đường thẳng
Ví dụ 1:
Cho đường thẳng a nằm trên mp(P) , đường thẳng b cắt (P) tại O và O không thuộc a . Vị trí tương đối của a và b là
Lời giải:
.
Ví dụ 2:
Trong không gian cho ba đường thẳng phân biệt a,b,c trong đó a song song với b . Khẳng định nào sau đây sai?
Lời giải:
.
3. Luyện tập củng cố: Đường thẳng song song đường thẳng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay