1. Bài giảng: Đường thẳng song song mặt phẳng
Đường thẳng song song mặt phẳng
1. Đường thẳng song song mặt phẳng
- Cho đường thẳng a và mặt phẳng (P). Khi đó có thể xảy ra một trong ba trường hợp sau:
- Trường hợp 1: a và (P) có từ hai điểm chung phân biệt trở lên (Hình 2a ), suy ra mọi điểm thuộc a đều thuộc (P), ta nói a nằm trong (P), ki hiệu a⊂(P).
- Trường hợp 2: a và (P) có một điểm chung duy nhất A (Hình 2b), ta nói a cắt (P) tại A, kí hiệu a∩(P)=A.
- Trường hợp 3: a và (P) không có điểm chung nào (Hình 2c), ta nói a song song với (P), kí hiệu a//(P).
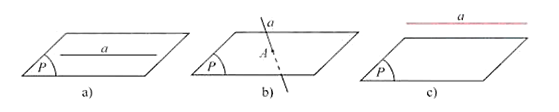
- Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.
2. Điều kiện để một đường thẳng song song với 1 mặt phẳng
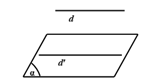
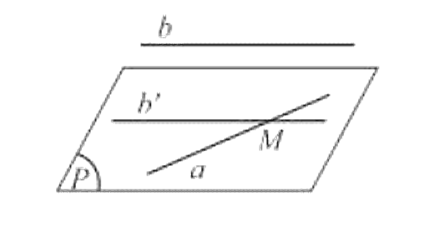
- Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d′ nằm trong (α) thì d song song với (α).
- Vậy ⎩⎪⎨⎪⎧d⊂(α)d∥d′d′⊂(α)⇒d∥(α)
3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
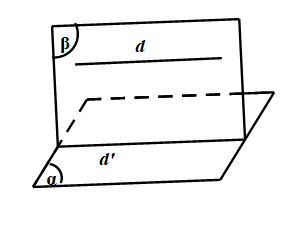
- Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β) đi qua d và cắt (α) theo giao tuyến d′ thì d′∥d
- Vậy ⎩⎪⎨⎪⎧d∥(α)d⊂(β)(α)∩(β)=d′⇒d′∥d
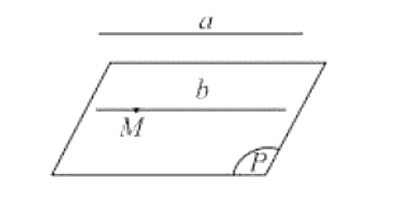
- Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
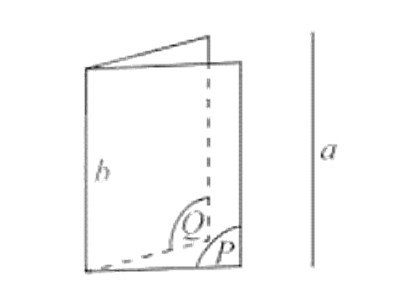
- Nếu a và b là hai đường thẳng chéo nhau thì qua a có duy nhất một mặt phẳng song song với đường thẳng b
2. Ví dụ minh hoạ: Đường thẳng song song mặt phẳng
Ví dụ 1:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N là hai điểm trên SA,SB sao cho SASM=SBSN=31 .
Vị trí tương đối giữa MN và (ABCD) là:
Lời giải:
Theo định lí Talet, ta có SASM=SBSN suy ra MN song song với AB .
Mà AB nằm trong mặt phẳng (ABCD) suy ra MN // (ABCD) .
Ví dụ 2:
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
Gọi O , O1 lần lượt là tâm của ABCD , ABEF M là trung điểm của CD .
Khẳng định nào sau đây sai?
Lời giải:


Xét tam giác ACE có O,O1 lần lượt là trung điểm của AC , AE .
Suy ra OO1 là đường trung bình trong tam giác ACE ⇒OO1 // EC .
Tương tự, OO1 là đường trung bình của tam giác BFD nên OO1 // FD .
Vậy OO1 // (BEC) , OO1 // (AFD) và OO1 // (EFC) . Chú ý rằng: (EFC)=(EFM) .
3. Luyện tập củng cố: Đường thẳng song song mặt phẳng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay