1. Bài giảng: Hàm Số Lượng Giác và Đồ Thị
Hàm số lượng giác và đồ thị
1. Hàm số chẵn, hàm số lẻ
Cho hàm số y=f(x) với tập xác định D.
- Hàm số y=f(x) được gọi là hàm số chẵn nếu ∀x∈D thì −x∈D và f(−x)=f(x).
- Hàm số y=f(x) được gọi là hàm số lẻ nếu ∀x∈D thì −x∈D và f(−x)=−f(x).
Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng, đồ thị hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
2. Hàm số tuần hoàn
Cho hàm số y=f(x) với tập xác định D. Hàm số y=f(x) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x∈D, ta có:
- x+T∈D và x−T∈D;
- f(x+T)=f(x).
Số T dương nhỏ nhất (nếu có) thoả mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
3. Một số hàm số lượng giác cơ bản
a) Hàm số y=sinx
- Hàm số y=sinx có tập xác định là R; tập giá trị là đoạn [−1;1].
- Đồ thị hàm số y=sinx được biểu diễn ở Hình 5 :
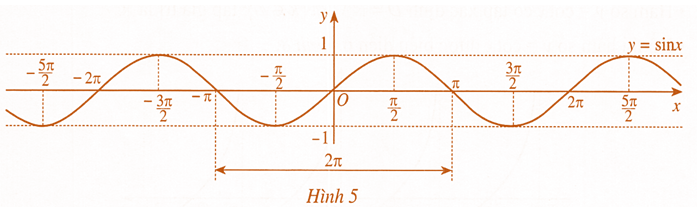
Hàm số y=sinx là hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ O; tuần hoàn chu kì 2π; đồng biến trên mỗi khoảng (−2π+k2π;2π+k2π) và nghịch biến trên mỗi khoảng (2π+k2π;23π+k2π) với k∈Z.
b) Hàm số y=cosx
Hàm số y=cosx có tập xác định là R; tập giá trị là đoạn [−1;1].
Đồ thị hàm số y=cosx được biểu diễn ở Hình 6 :
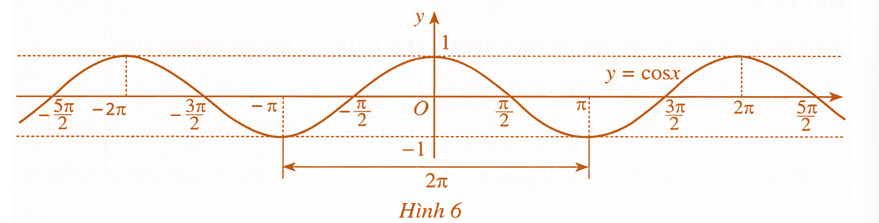
Hàm số y=cosx là hàm số chẵn, có đồ thị đối xứng qua trục tung; tuần hoàn chu kì 2π; đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π) với k∈Z.
c) Hàm số y=tanx
Hàm số y=tanx có tập xác định là D=R\{2π+kπ∣k∈Z} tập giá trị là R.
Đồ thị hàm số y=tanx được biểu diễn ở Hình 7:
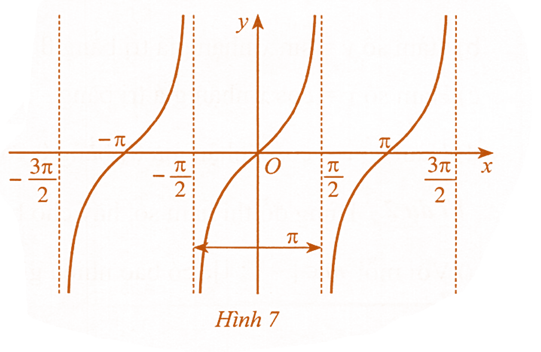
Hàm số y=tanx là hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ O; tuần hoàn chu kì π; đồng biến trên mỗi khoảng (−2π+kπ;2π+kπ) với k∈Z.
d) Hàm số y=cotx
Hàm số y=cotx có tập xác định D=R\{kπ∣k,∈Z}; tập giá trị là R.
Đồ thị hàm số y=cotx được biểu diễn ở Hình 8 :
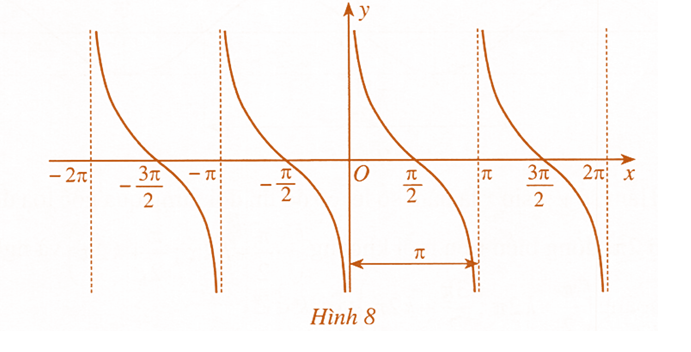
Hàm số y=cotx là hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ O; tuần hoàn chu kì π; nghịch biến trên mỗi khoảng (kπ;π+kπ) với k∈Z.
2. Ví dụ minh hoạ: Hàm Số Lượng Giác và Đồ Thị
Ví dụ 1:
Sử dụng đồ thị ở hình dưới, xác định các giá trị x trên đoạn [−2π;23π] để hàm số y=sinx nhận giá trị bằng 0

Lời giải:
Dựa vào đồ thị hàm số, xác định các điểm giao với trục hoành => x∈{0;π}
Ví dụ 2:
Sử dụng đồ thị ở hình dưới, hàm số y=sinx đồng biến trên khoảng nào dưới đây

Lời giải:
Dựa vào đồ thị hàm số, xác định khoảng mà đồ thị chỉ đi lên => x∈(−2π;0)
3. Luyện tập củng cố: Hàm Số Lượng Giác và Đồ Thị
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay