1. Bài giảng: Phép quay
Phép quay
1. Khái niệm
Cho điểm O cố định và số thực α∘.
Phép quay thuận chiều α∘(0∘<α∘<360∘) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O ) thành điểm M′ thuộc đường tròn (O;OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM′ thì điểm M tạo nên cung MN′ có số đo α∘. Định nghĩa tương tự cho phép quay ngược chiều α∘ tâm O.
Phép quay 0∘ và phép quay 360∘ giữ nguyên mọi điểm.
2. Phép quay giữ nguyên hình đa giác đều
Cho hình đa giác đều A1A2...An(n≥3,n∈N) có tâm O. Phép quay giữ nguyên hình đa giác là phép quay tâm O biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đó đều đó.
Người ta chứng minh được rằng chỉ có các phép quay sau đây giữ nguyên hình đa giác đều A1A2...An(n≥3,n∈N) với tâm O: các phép quay thuận chiều α∘ tâm O và các phép quay ngược chiều α∘ tâm O, với α∘ lần lượt nhận các giá trị:
α∘=n360∘;α∘=n2⋅360∘;...;α∘=nn⋅360∘=360∘
2. Ví dụ minh hoạ: Phép quay
Ví dụ 1:
Cho hình vuông ABCD có tâm O (Hình vẽ). Phép quay thuận chiều tâm O biến điểm A thành điểm D, biến điểm C biến thành điểm nào?
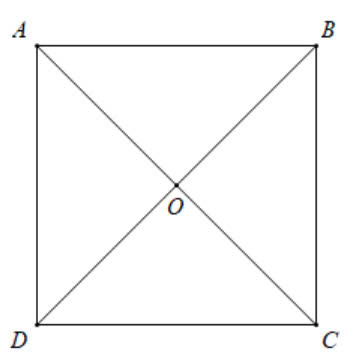
Lời giải:
Các góc ở tâm của hình vuông là 360:4=90°
Phép quay thuận chiều tâm O biến điểm A thành điểm D
Suy ra đây là phép quay thuận chiều 90°⋅3=270°
Khi đó phép quay này biến điểm C thành điểm B.
Ví dụ 2:
Cho hình vuông ABCD có tâm O (Hình vẽ). Phép quay thuận chiều tâm O biến điểm A thành điểm D, biến điểm B biến thành điểm nào?

Lời giải:
Các góc ở tâm của hình vuông là 360:4=90°
Phép quay thuận chiều tâm O biến điểm A thành điểm D
Suy ra đây là phép quay thuận chiều 90°⋅3=270°
Khi đó phép quay này biến điểm B thành điểm A.
3. Luyện tập củng cố: Phép quay
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay