1. Bài giảng: GTLN-GTNN của hàm số
GTLN-GTNN của hàm số
1. Định nghĩa giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Định nghĩa: Cho hàm số y=f(x) xác định trên tập D. Khi đó ta có:
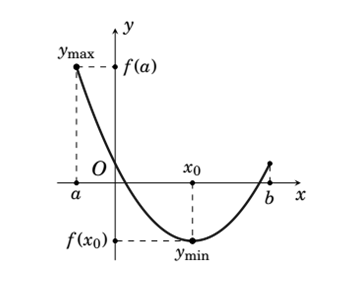
- M là giá trị lớn nhất của hàm số nếu {f(x)≤M,∀x∈D∃x0∈D:f(x0)=M . Kí hiệu x∈Dmaxf(x)=M.
- m là giá trị nhỏ nhất của hàm số nếu {f(x)≥m,∀x∈D∃x0∈D:f(x0)=m . Kí hiệu x∈Dminf(x)=m.
2. Một số lưu ý
- Khi yêu cầu tìm max min của hàm số mà không nói rõ xét trên tập nào thì ta hiểu là tìm max min trên miền xác định của hàm số đó.
- Để tìm max min của hàm số y=f(x) trên miền D ta thường lập bảng biến thiên của hàm số y=f(x) trên D. Từ bảng biến thiên ta có thể kết luận:
Điểm ở vị trí cao nhất Kết luận max
Điểm ở vị trí thấp nhất Kết luận min
- Để tìm max min của hàm số y=f(x) trên đoạn [a;b] (f(x) liên tục trên đoạn [a;b] và có đạo hàm trên (a;b) có thể trừ một số hữu hạn các điểm và f′(x)=0 chỉ tại một số hữu hạn điểm trong (a;b) ) thì ta có thể giải theo các bước sau:
Bước 1: Giải phương trình f′(0) tìm các nghiệm x0∈(a;b)
Bước 2: Tìm các điểm xi∈(a;b) mà tại đó đạo hàm không xác định (nếu có)
Bước 3: Tính toán f(a),f(x0),f(xi),f(b)(∗)
Bước 4: Gọi M,m lần lượt là số lớn nhất và số nhỏ nhất của các kết quả tính toán ở bước (∗) thì ta có thể kết luận: M=[a;b]maxf(x);m=[a;b]minf(x)
Ta có thể sử dụng các bất đẳng thức có sẵn để đánh giá biểu thức cần tìm max, min.
- Bất đẳng thức Cauchy cho hai số không âm a,b:
a+b≥2√ab
Dấu ′′=′′ xảy ra khi a=b
- Bất đẳng thức Cauchy cho ba số không âm a,b,c:
a+b+c≥33√abc
Dấu ′′=′′ xảy ra khi a=b=c
- Bất đẳng thức Cauchy cho n số không âm a1,a2,...,an:
a1+a2+...+an≥nn√a1a2...an
Dấu ′′=′′ xảy ra khi a1=a2=...=an
2. Ví dụ minh hoạ: GTLN-GTNN của hàm số
Ví dụ 1:
Cho hàm số y=f(x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Lời giải:
Hàm số liên tục và giảm trên đoạn [0;2] nên hàm số y=f(x) đạt GTLN tại x=0 .
Ví dụ 2:
Cho hàm số y=f(x) xác định và liên tục trên khoảng (−∞;1) và (1;+∞) và có đồ thị như hình vẽ. Mệnh đề nào sau đây là đúng

Lời giải:
Hàm số liên tục và tăng trên đoạn [−2;0] nên [−2;0]maxf(x)=f(0)
3. Luyện tập củng cố: GTLN-GTNN của hàm số
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay