VECTOR

A. KHÁI NIỆM VECTOR

1. Định nghĩa vectơ

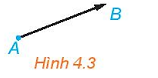
• Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.
• Vectơ có điểm đầu A, điểm cuối B được kí hiệu là AB, đọc là vectơ AB 
• Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ AB. 
• Độ dài của đoạn thẳng AB gọi là độ dài của vectơ AB và được thành kí hiệu là ∣∣∣∣​AB∣∣∣∣​. Như vậy ta có: ∣∣∣∣​AB∣∣∣∣​=AB. 

2. Hai vectơ cùng phương, cùng hướng

Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là a⃗,b⃗,x⃗,y⃗​,…

Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

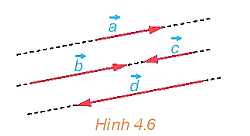
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

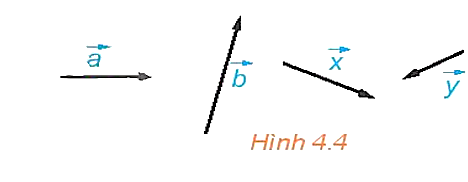
Nhận xét: Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

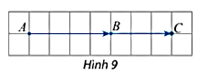
Ba điểm phân biệt A,B,C thẳng hàng khi và chỉ khi hai vectơ AB và AC cùng phương.

Nếu ba điểm phân biệt A,B,C thẳng hàng thì hai vectơ AB và AC cùng hướng.

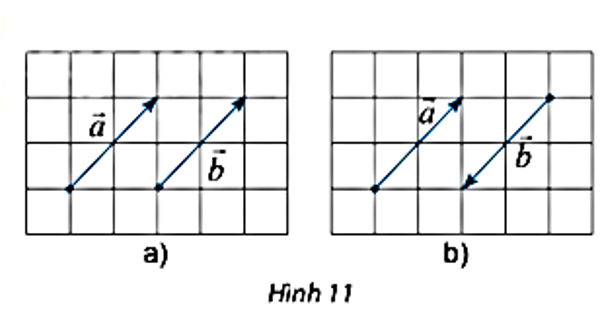
3. Vectơ bằng nhau

• Vectơ đối nhau Hai vectơ a⃗ và b⃗  được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài
• Kí hiệu a⃗=b⃗.  
• Hai vectơ a⃗  và b⃗  được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu a⃗=−b⃗. Khi đó, vectơ b⃗ được gọi là vectơ đối của vectơ a⃗.  

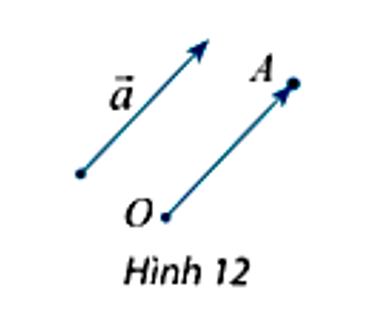
Chú ý: Cho vectơ a⃗  và điểm O, ta luôn tìm được một điểm A duy nhất sao cho OA=a⃗. Khi đó độ dài của vectơ a⃗  là độ dài đoạn OA, kí hiệu là ∣a⃗∣. Cho đoạn thẳng MN, ta luôn có NM=−MN.  

4. Vectơ-không

Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là 0⃗. 

Chú ý: Quy ước vectơ- không có độ dài bằng 0.

Vectơ- không luôn cùng phương, cùng hướng với mọi vectơ.

Mọi vectơ không đều bằng nhau: 0⃗=AA=BB=CC=… với mọi điểm A,B,C,… 

Vectơ đối của vectơ-không là chính nó.

B. TỔNG HIỆU CỦA HAI VECTOR

1. Tổng của hai vectơ

Cho hai vectơ a⃗  và b⃗ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho AB  = a⃗ , BC  = b⃗ . Khi đó AC  được gọi là tổng của hai vectơ a⃗ , b⃗  và được kí hiệu là a⃗  + b⃗ .

Vậy a⃗  + b⃗  = AB + BC  = AC .

Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.

Từ định nghĩa tổng của hai vectơ, ta suy ra quy tắc cộng vectơ sau đây:

Quy tắc ba điểm

Với ba điểm M, N, P, ta có: MN  + NP  = MP  .

Quy tắc hình bình hành

Nếu OABC là hình bình hành thì ta có OA  + OC  = OB .

Chú ý: Khi cộng hai vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

Để áp dụng quy tắc hình bình hành, ta cần đưa bài toán tìm tổng hai vectơ về bài toán tìm tổng của hai vectơ có chung điểm đầu.

2. Tính chất của phép cộng các vectơ

Cho ba vectơ a⃗ , b⃗ , c⃗  được biểu diễn như

Phép cộng vectơ có các tính chất sau:

Tính chất giao hoán: a⃗  + b⃗  = b⃗  + a⃗ ;

Tính chất kết hợp: (a⃗  + b⃗ ) + c⃗  = a⃗  + (b⃗  + c⃗ );

Với mọi vectơ a⃗ , ta luôn có: a⃗  + 0⃗  = 0⃗  + a⃗  = a⃗ .

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ a⃗ , b⃗ , c⃗ , kí hiệu là c⃗  với a⃗  + b⃗  + c⃗  = (a⃗  + b⃗ ) + c⃗ .

3. Hiệu của hai vectơ

Vectơ a+(−b) được gọi là hiệu của hai vec tơ a và b và được kí hiệu là a−b . Phép lấy hiệu hai vec tơ được gọi là phép trừ vec tơ.

Quy tắc hiệu: Với ba điểm O,M,N  ta có MN=ON−OM. 

4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Khi I là trung điểm của AB, thì hai vec tơ IA và IB có cùng độ dài và ngược hướng.

Do đó, IA và IB đối nhau, suy ra IA+IB=0. 

Trọng tâm G của tam giác ABC  thuộc trung tuyến AI và GA=2GI. Lấy điểm D đối xứng với G qua I. 

 GA+GB+GC=0. 

C. TÍCH CỦA MỘT SỐ VỚI VECTOR

1. Tích của một số với một vectơ

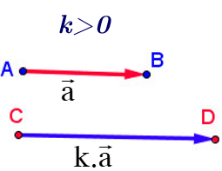
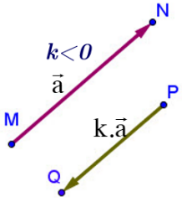
• Cho số k khác 0 và vectơ a⃗  khác 0⃗. Tích của số k với vectơ a⃗  là một vectơ, kí hiệu là ka⃗.   
•  Vectơ ka⃗ cùng hướng với a⃗  nếu k>0, ngược hướng với a⃗  nếu k<0 và có độ dài bằng ∣k∣.∣a∣. 

• Ta quy ước 0a⃗ và k0⃗=0⃗.
• Người ta còn gọi tích một số với một vectơ là tích của một vectơ với một số.

2. Tính chất 

Với hai vectơ a⃗  và b⃗  bất kì, với mọi số thực t và k, ta có: k (a⃗  +b⃗ ) = ka⃗  + kb⃗ ; (t + k)a⃗  = ta⃗  + ka⃗ ; t(ka⃗ ) = (tk)a⃗ ; 1.a⃗  = a⃗ . (- 1).a⃗  = -a⃗ .

3. Điều kiện để hai vectơ cùng phương 

Hai vectơ a⃗  và b⃗  (b⃗  khác 0⃗ ) cùng phương khi và chỉ khi có số k sao cho a⃗  = kb⃗ . Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để AB  = kAC .

Chú ý: Cho hai vectơ a⃗  và b⃗  không cùng phương. Với mọi vectơ c⃗  luôn tồn tại duy nhất cặp số thực (m; n) sao cho c⃗  = ma⃗  + nb⃗ .

4. Ứng dụng:

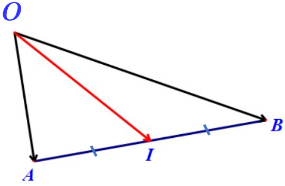
Cho đoạn thẳng AB có trung điểm I. Với điểm O tùy ý, ta có: OA+OB=2OI. 

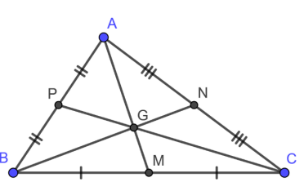
Cho tam giác ABC có trọng tâm G. Với điểm O tùy ý, ta có OA+OB+OC=3OG.