HỆ THỨC LƯỢNG TRONG TAM GIÁC

I. Giá trị lượng giác của một góc

1. Định nghĩa:

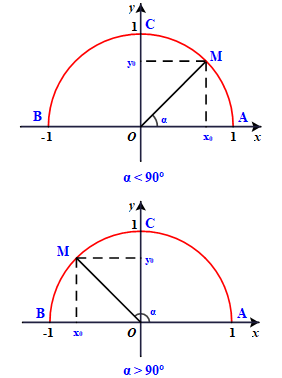
Với mỗi góc α (00≤α≤1800) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho xOM=α và giả sử điểm M có tọa độ M(x0​;y0​). 

Khi đó ta có định nghĩa:

sin của góc α là y0​, kí hiệu sinα=y0​;  cosin của góc α là x0​, kí hiệu cosα=x0​;  tang của góc α là x0​y0​​(x0​=0),  kí hiệu tanα=x0​y0​​;  côtang của góc α là y0​x0​​(y0​=0),  kí hiệu cotα=y0​x0​​.

Từ định nghĩa trên, ta có:

2. Tính chất:

Hai góc bù nhau: Trên hình bên ta có dây cung NM song song với trục Ox  và nếu xOM=α thì xON=180∘−α. Ta có yM​=yN​=y0​,xM​=−xN​=x0​. Do đó

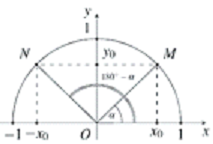
sin(180∘−α)=sinα                                 cos(180∘−α)=−cosα 

tan(180∘−α)=−tanα                             cot(180∘−α)=cotα 

II. Hệ thức lượng trong tam giác

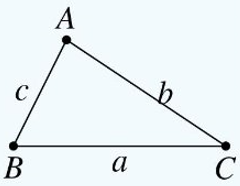
1. Định lý Côsin

Cho tam giác ABC  có BC=a,AC=b  và AB=c. Ta có

• a2=b2+c2−2bccosA. 
• b2=c2+a2−2cacosB. 
• c2=a2+b2−2abcosC. 

Hệ quả: Áp dụng để tính góc

• cosA=2bcb2+c2−a2​. 
• cosB=2cac2+a2−b2​. 
•  cosC=2aba2+b2−c2​. 

2. Định lý sin:

Tam giác ABC với BC=a,CA=b,AB=c và R là bán kính đường tròn ngoại tiếp, ta có: sinAa​=sinBb​=sinCc​=2R 

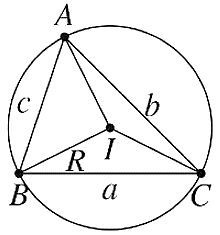
3. Công thức tính diện tích tam giác

Cho tam giác ABC có

• ha​,hb​,hc​ là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB; 
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• p=2a+b+c​  là nửa chu vi tam giác;
• S là diện tích tam giác. Khi đó ta có:

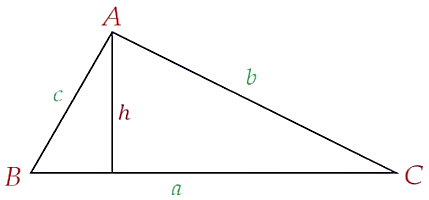
• S=21​a⋅ha​=21​b⋅hb​=21​c⋅hc​. 
• S=21​bcsinA=21​casinB=21​absinC 
• S=4Rabc​. 
• S=p⋅r 
• S=√p(p−a)(p−b)(p−c)​.