1. Bài giảng: Tập Hợp
Tập hợp
1. Tập hợp
2. Tập con và hai tập hợp bằng nhau
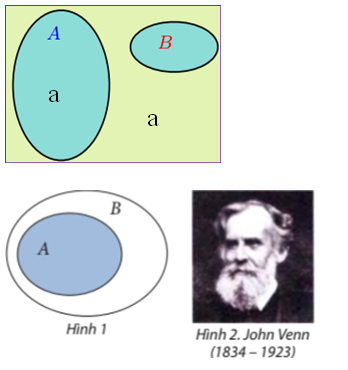
- Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A⊂B (đọc là A chứa trong B), hoặc B⊃A (đọc là B chứa A)
- A⊂A và ∅⊂A với mọi tập hợp A.
- Nếu A không phải là tập con của B thì ta kí hiệu A⊂B (đọc là A không chứa trong B hoặc B không chứa A ).
- Nếu A⊂B hoặc B⊂A thì ta nói A và B có quan hệ bao hàm.
3. Hai tập hợp bằng nhau
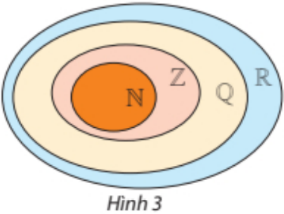
4. Các tập hợp số đã học
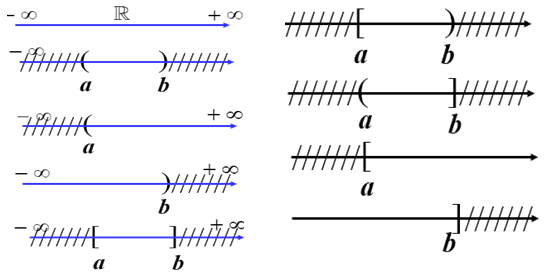
5. Các tập con thường dùng của R:
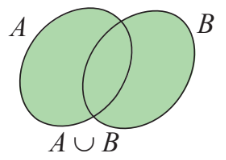
6. Hợp của hai tập hợp
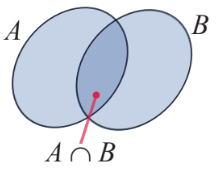
7. Giao của hai tập hợp
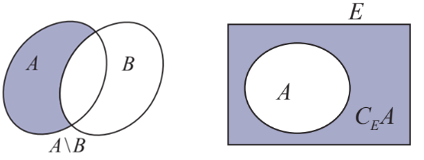
8. Hiệu và phần bù của hai tập hợp
2. Ví dụ minh hoạ: Tập Hợp
Ví dụ 1:
ChoA={1;2;3} .
Trong các khẳng định sau, khẳng địng nào sai?
Lời giải:
∅⊂A đúng do tập ∅ là tập con của mọi tập hợp.
1∈A đúng do 1 là một phần tử của tập A .
{1;2}⊂A đúng do tập hợp có chứa hai phần tử {1;2} là tập con của tập A .
2=A sai do số 2 là một phần tử của tập A thì không thể bằng tập A .
Ví dụ 2:
Trong các mệnh đề sau, tìm mệnh đề nào sai?
Lời giải:
A∈A sai do tập A thì không thể là phần tử của tậpA (sai ký hiệu).
∅⊂A đúng do tập ∅ là tập con của mọi tập hợp.
A⊂A đúng do tậpA là tập con của chính nó.
A={A} đúng do tập hợp có chứa một phần tử {A} thì không thể bằng tậpA .
{Với A là tập hợp}
3. Luyện tập củng cố: Tập Hợp
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay