1. Bài giảng: Khoảng cách
Khoảng cách
1. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG, ĐẾN MỘT MẶT PHẲNG
- Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dại đoạn MH được gọi là khoảng cách từ M đến đường thẳng a, kí hiệu d(M,a). Vậy d(M,a)=MH.
- Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dại đoạn MH được gọi là khoảng cách từ M đến mặt phẳng (P) , kí hiệu d(M,(P)). Vậy d(M,(P))=MH
- Ta quy ước: d(M,a)=0 khi và chỉ khi M thuộc a,
- d(M,(P))=0 khi và chỉ khi M thuộc (P).
a) Lấy điểm N tuỳ ý trên đường thẳng a, ta luôn có d(M,a)≤MN.
b) Lấy điểm N tuỳ ý trên mặt phẳng (P), ta luôn có d(M,(P))≤MN.
2. KHOẢNG CÁCH GIỮA CÁC ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG. KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG
- Khoảng cách giữa hai đường thẳng song song a và b là khoảng cách từ một điểm bất kì trên a đến b, kí hiệu d(a,b).
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P), kí hiệu d(a,(P)).
- Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì trên (P) đến (Q), kí hiệu d((P),(Q)).
3. KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
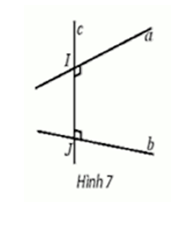
- Đường thẳng c vừa vuông góc, vưa cắt hai đường thẳng chéo nhau a và b được gọi là đường vuông góc chung của a và b.
- Nếu dường vuông góc chung của hai đường thẳng chéo nhau a và b cắt chúng lần lươt tại I và J thì đoạn IJ gọi là đoạn vuông góc chung của a và b.
- Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a,b).
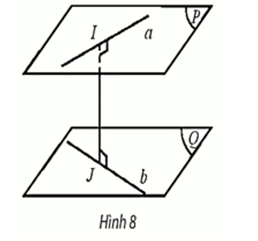
- Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường đến mặt phẳng song song với nó và chứa đường còn lại.
- Khoảng cách giũa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
.
2. Ví dụ minh hoạ: Khoảng cách
Ví dụ 1:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng
Lời giải:

Gọi H là trung điểm của BC nên
AH=2BC=2a,SH⊥(ABC),SH=2a√3.
Gọi K là hình chiếu vuông góc của H trên SA⇒HK⊥SA.
Ta có: BC⊥(SAH)⇒BC⊥HK⇒d(SA;BC)=HK.
Xét tam giác SHA vuông tại H.
Ta có HK21=SH21+AH21=3a216⇒HK=4a√3.
Vậy d(SA;BC)=4a√3.
Ví dụ 2:
Cho hình chóp S.ABCD có cạnh đáy SA vuông góc với đáy, ABCD là hình vuông cạnh a .
Biết góc giữa SB và mặt đáy bằng 60o .
Khoảng cách giữa hai đường thẳng BD và SC bằng
Lời giải:

Do SA⊥(ABCD) nên (SB;(ABCD))=SBA=60o.
Do tam giác SAC vuông tại A nên
SA=AB.tanSBA=a√3.
Gọi O là tâm hình vuông ABCD.
Ta có: {BD⊥ACBD⊥SA⇒BD⊥(SAC).
Trong mặt phẳng (SAC) , dựng OH⊥SC.
Suy ra d(BD;SC)=OH.
Dựng AK//OH⇒OH=21AK.
Xét tam giác SAC vuông tại A:
AK21=AS21+AC21=6a25⇒AK=5√30a.
Vậy d(BD;SC)=5√30a.
3. Luyện tập củng cố: Khoảng cách
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay