Hai mặt phẳng vuông góc

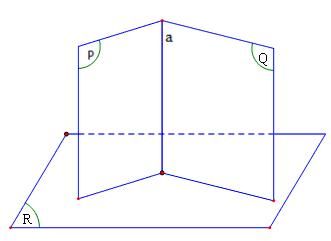
1. GÓC GIỮA HAI MẶT PHẲNG

Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

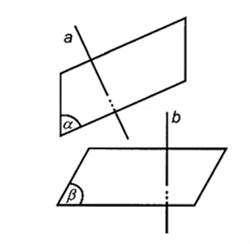
 ​a⊥(α)b⊥(β)​}⇒((α),(β)​)=(a,b​).  

2. HAI MẶT PHẲNG VUÔNG GÓC

Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc với nhau nếu góc giữa chúng bằng 90∘. 

• (P)⊥(Q)⇔((P),(Q))⌢​=90∘ 

Chú ý: (α)//(β)⇒((α),(β)​)=0o;  (α)≡(β)⇒((α),(β)​)=0o. 

Cách xác định góc khác: Dùng cho hai mặt phẳng cắt nhau: “Góc giữa hai mặt phẳng là góc giữa hai đường thẳng cùng vuông góc với giao tuyến tại một điểm”.

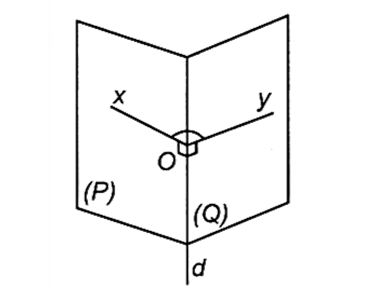
Bước 1. Tìm giao tuyến d của (P)  và (Q). 

Bước 2. Chọn điểm O trên d, từ đó:

+) Trong (P)  dựng Ox⊥d. 

+) Trong (Q)  dựng Oy⊥d. 

• Khi đó: ((α),(β))​=(Ox,Oy)​. 

Lưu ý: Việc xác định điểm O có thể được thực hiện theo cách sau: Chọn điểm M trên (Q)  sao cho dễ dàng xác định hình chiếu H của nó trên (P).  Dựng MO⊥d  thì khi đó ((α),(β))​=MOH. 

Điều kiện hai mặt phẳng vuông góc

Định lý 1: Hai mặt phẳng vuông góc với nhau khi và chỉ khi trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia.

{​a⊂(P)a⊥(Q)​⇒(P)⊥(Q).    

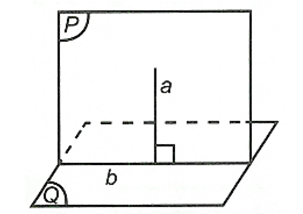
3. TÍNH CHẤT CƠ BẢN VỀ HAI MẶT PHẲNG VUÔNG GÓC

Định lý 2: Với hai mặt phẳng vuông góc với nhau, bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

⎩⎪⎪⎪⎨⎪⎪⎪⎧​​(P)⊥(Q)a⊂(P)b=(P)∩(Q)a⊥b​⇒a⊥(Q).  

Nhận xét: Cho hai mặt phẳng (P)  và (Q)  vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (P)  dựng một đường thẳng vuông góc với mặt phẳng (Q)  thì đường thẳng này nằm trong (P) .

⎩⎪⎨⎪⎧​​A∈(P)(P)⊥(Q)A∈a⊥(Q)​⇒a⊂(P).  

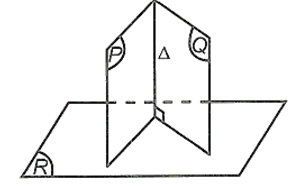
Định lý 3: Nếu hai mặt phẳng cắt nhau cùng vuông góc với một mặt phẳng thứ 3 thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ 3.

⎩⎪⎨⎪⎧​​(P)⊥(R)(Q)⊥(R)(P)∩(Q)=Δ​⇒Δ⊥(R).