1. Bài giảng: Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
Góc giữa đường thẳng và mặt phẳng góc nhị diện
1. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
- Cho đường thẳng a và mặt phẳng (P).
- Nếu a vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 90∘.
- Nếu a không vuông góc với mặt phẳng (P) thì góc giữa a với hình chiếu a′ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
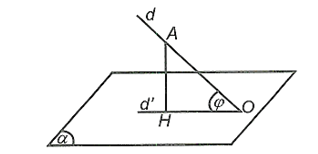
- Góc giữa đường thẳng a và mặt phẳng (P) được kí hiệu (a,(P))
- Nếu α là góc giữa đường thẳng a và mặt phẳng (P) thì 0∘≤α≤90∘.
- Nếu đường thẳng a nằm trong mặt phẳng (P) hoặc song song với mặt phẳng (P) thì (a,(P))=0∘.
2. GÓC NHỊ DIỆN VÀ GÓC PHẲNG NHỊ DIỆN
a) Góc nhị diện
- Cho hai nửa mặt phẳng (P1) và (Q1) có chung bờ là đường thẳng d . Hình tạo bởi (P1) , (Q1) và d được gọi là góc nhị diện tạo bởi (P1) và (Q1) , kí hiệu [P1,d,Q1].
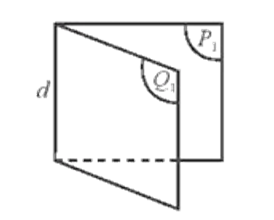
- Hai nửa mặt phẳng (P1) , (Q1) gọi là hai mặt của nhị diện và d gọi là cạnh của nhị diện
- Hai mặt phẳng cắt nhau theo giao tuyến d tạo thành bốn góc nhị diện.
- Góc nhị diện [P1,d,Q1] còn được ki hiệu là [M,d,N] với M,N tương ưng thuộc hai nưa mặt phẳng (P1),(Q1).
b) Góc phẳng nhị diện
- Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
- Đối với một góc nhị diện, các góc phẳng nhị diện đều bằng nhau.
- Nếu mặt phẳng (R) vuông góc với cạnh d của góc nhị diện và cắt hai mặt (P1),(Q1) của góc nhị diện theo hai nửa đường thẳng Ou và Ov thi uOv là góc phẳng nhị diện của góc nhị diện tạo bởi (P1),(Q1).
- Góc nhỉ diện có góc phẳng nhỉ diện là góc vuông được gọi là góc nhị diện vuông.
- Số đo góc phẳng nhị diện được gọi là số đo góc nhị diện.
- Số đo góc nhị diện nhận giá trị từ 0∘ đến 180∘.
.
2. Ví dụ minh hoạ: Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
Ví dụ 1:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a , ABC=600 , SA=a√3 và SA⊥(ABCD) .
Tính góc giữa SA và mặt phẳng (SBD) .
Lời giải:


Gọi O là tâm của hình thoi ABCD , gọi H là hình chiếu vuông góc của A lên SO , ta có:
{BD⊥ACBD⊥SA⇒BD⊥(SAC)⇒BD⊥AH .
Từ AH⊥SO,AH⊥BD suy ra AH⊥(SBD) , hay SH là hình chiếu vuông góc của SA lên (SBD) ,
Suy ra (SA,(SBD))=(SA,SO)=ASO .
Ta có ΔABC đều cạnh 2a nên OA=a .
ΔSAO vuông tại A nên tanASO=SAOA=√31⇒AOS=30∘ .
Ví dụ 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh bằng 4a , cạnh bên SA=3a .
Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trung điểm H của đoạn thẳng AO .
Gọi α là góc giữa đường thẳng SH và mặt phẳng (SBD) .
Tính sinα .
Lời giải:


Ta có: SH⊥(ABCD) , gọi K là hình chiếu của điểm H xuống cạnh SO .
Do {BD⊥AOBD⊥SH⇒BD⊥(SHO)⇒BD⊥HK .
Khi đó{HK⊥SOHK⊥BD⇒HK⊥(SBD) , suy ra KS là hình chiếu SH xuống mặt phẳng (SBD) . Do đó góc giữa đường thẳng SH và mặt phẳng (SBD) bằng HSK .
AH=HO=a√2;SH=a√7;HK=√SH2+SO2SH.HO=3a√14
Trong tam giác HKS , sinHSK=SHHK=3a√14:a√7=3√2 .
3. Luyện tập củng cố: Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay