1. Bài giảng: Góc và Giá trị của góc lượng giác
GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
1. Khái niệm góc lượng giác và số đo của góc lượng giác
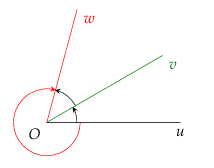
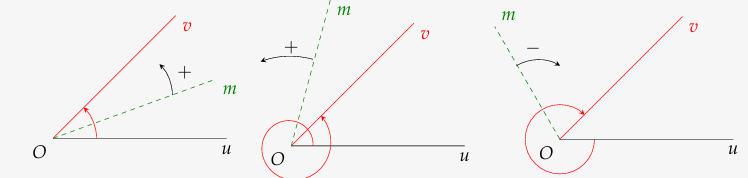
Khái niệm 1.1. Trong mặt phẳng, cho hai tia Ou,Ov. Xét tia Om cùng nằm trong mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou, tia cuối Ov và kí hiệu là (Ou,Ov). Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của nó.
3. Đơn vị đo góc và cung tròn
Mối quan hệ giữa độ và rađian
Quan hệ giữa độ và rađian: Do đường tròn có độ dài là 2πR nên nó có số đo 2π rad. Mặt khác, đường tròn có số đo bằng 360∘ nên ta có 360∘=2π rad.
Do đó ta viết:
1∘=180∘π rad và 1 rad =(π180)∘
Khi viết số đo của một góc theo đơn vị rađian, người ta thường không viết chữ rad sau số đo. Chẳng hạn góc 2π được hiểu là góc 2π rad.
4. Độ dài cung tròn
Định nghĩa 1.1. Một cung của đường tròn bán kính R và có số đo α rad thì có độ dài l=Rα.
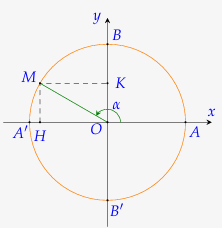
5. Đường tròn lượng giác.
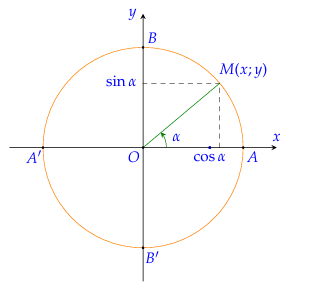
6. Các giá trị lượng giác của góc lượng giác
a) Ta còn gọi trục tung là trục sin, trục hoành là trục côsin.
b) Từ định nghĩa ta suy ra:
+ sinα,cosα xác định với mọi giá trị của α và ta có:
+ −1≤sinα≤1;−1≤cosα≤1
+ sin(α+k2π)=sinα;cos(α+k2π)=cosα(k∈Z).
+ tanα xác định khi α=2π+kπ(k∈Z).
+ cotα xác định khi α=kπ(k∈Z).
+ Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn M trên đường tròn lượng giác.
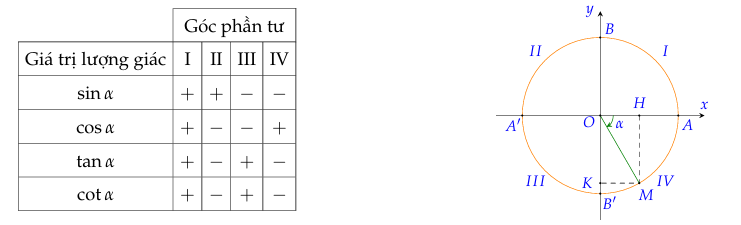
7. Giá trị lượng giác của góc đặc biệt
| Góc α |
0 |
6π |
4π |
3π |
2π |
| 0° |
30° |
45° |
60° |
90° |
|
|
sinα |
0 | 21 | 2√2 | 2√3 | 1 |
| cosα | 1 | 2√3 | 2√2 | 21 | 0 |
| tanα | 0 | √31 | 1 | √3 | Không xác định |
| cotα | Không xác định | √3 | 1 | √31 | 0 |
8. Sử dụng máy tính cầm tay để đổi số đo góc và tìm giá trị lượng giác của góc
Có thể dùng máy tính cầm tay để tính giá trị lượng giác của góc lượng giác và đổi số đo độ của cung tròn rađian và ngược lại.
2. Ví dụ minh hoạ: Góc và Giá trị của góc lượng giác
Ví dụ 1:
Đổi số đo của góc 43 rad sang đơn vị độ, phút, giây.
Lời giải:
Sử dụng CASIO ta được kết quả 42058′18′′.
Ví dụ 2:
Đổi số đo của góc 1249π sang độ ta được kết quả bằng
Lời giải:
Áp dụng công thức chuyển đổi: 1249π=(π1249π.180)∘=735∘ .
3. Luyện tập củng cố: Góc và Giá trị của góc lượng giác
Học đi đôi với hành, luyện tập hàng ngày để trở nên thông thái
Luyện tập ngay